
题目列表(包括答案和解析)
1.(满分10分)某项选拔共有四轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考核,否则被淘汰。已知某选手能正确回答第一、二、三、四轮问题的概率分别为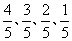 ,且各轮问题能否正确回答互不影响。
,且各轮问题能否正确回答互不影响。
(1)求该选手进入第四轮才被淘汰的概率; 

(2)求该选手至多进入第三轮考核的概率。
12. (Ⅰ)因为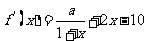
所以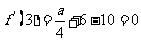
因此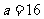
(Ⅱ)由(Ⅰ)知,
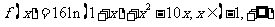
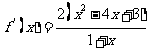
当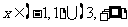 时,
时,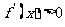
当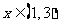 时,
时,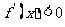
所以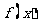 的单调增区间是
的单调增区间是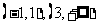
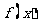 的单调减区间是
的单调减区间是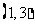
(Ⅲ)由(Ⅱ)知,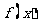 在
在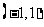 内单调增加,在
内单调增加,在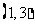 内单调减少,在
内单调减少,在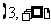 上单调增加,且当
上单调增加,且当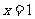 或
或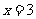 时,
时,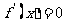
所以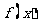 的极大值为
的极大值为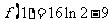 ,极小值为
,极小值为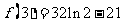
因此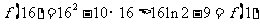

所以在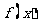 的三个单调区间
的三个单调区间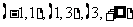 直线
直线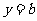 有
有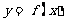 的图象各有一个交点,当且仅当
的图象各有一个交点,当且仅当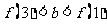
因此,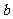 的取值范围为
的取值范围为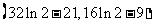 。
。
11. (I)解:由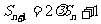 得
得
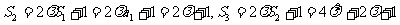 ,
,
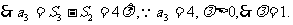
(II)由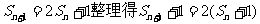 ,
,
∴数列{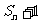 }是以S1+1=2为首项,以2为公比的等比数列,
}是以S1+1=2为首项,以2为公比的等比数列,
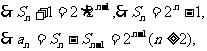
 当n=1时a1=1满足
当n=1时a1=1满足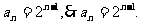
(III) ①
①
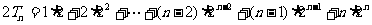 ,②
,②
①-②得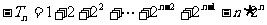 ,
,
则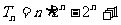 .
.
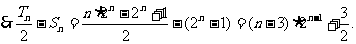
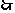 当n=1时,
当n=1时,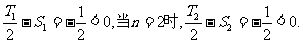
即当n=1或2时,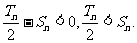
当n>2时,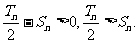
10. (1) 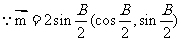 ,
,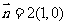 ,
,
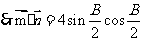 ,
,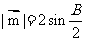 ,
,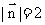 ,
,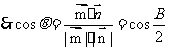
由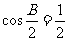 ,
,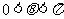 得
得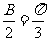 ,即
,即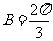
(2)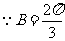 ,
,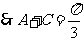

又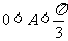 ,
,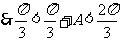 ,
,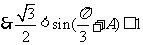 所以
所以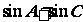
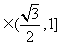
又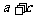 =
=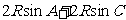 =
=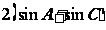 ,所以
,所以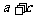
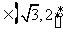 。
。
9. 解:(1)设第n年获取利润为y万元
n年共收入租金30n万元,付出装修费构成一个以1为首项,2为公差的等差数列,共
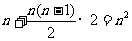 …………………………2分
…………………………2分
因此利润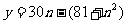 ,令
,令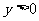 ……………………3分
……………………3分
解得: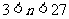 ,…………………………………….4分
,…………………………………….4分
所以从第4年开始获取纯利润 ………………………….5分
(2)纯利润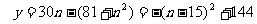
所以15后共获利润:144+ 10=154 (万元)………………………7分
年平均利润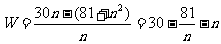 …………………..9分
…………………..9分
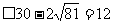 (当且仅当
(当且仅当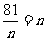 ,即n=9时取等号)……..10分
,即n=9时取等号)……..10分
所以9年后共获利润:12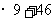 =154(万元)………………….11分
=154(万元)………………….11分
两种方案获利一样多,而方案②时间比较短,所以选择方案②……………12 分
8. (本小题满分14分) 

解:(1)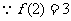 ,
,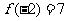 ,
,
由于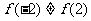 ,且
,且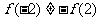 ,
,
故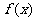 在
在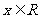 上既不是奇函数也不是偶函数;
............6分
上既不是奇函数也不是偶函数;
............6分
(2)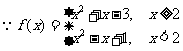 ,
.............8分
,
.............8分
当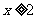 时,
时,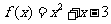 在
在 上单调递增,最小值为
上单调递增,最小值为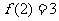 ,
,
当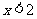 时,
时,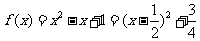 ,在
,在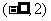 内的最小值为
内的最小值为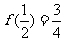 ,
,
故函数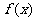 在
在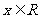 上的最小值为
上的最小值为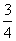 .
........14分
.
........14分
7. 解:(Ⅰ)因为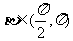 ,
,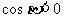 …………………………………………………………………2分
…………………………………………………………………2分
又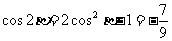 ,所以
,所以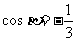 …………………………………………………6分(Ⅱ)根据(Ⅰ),得
…………………………………………………6分(Ⅱ)根据(Ⅰ),得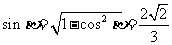 …………………………………………………… 8分而
…………………………………………………… 8分而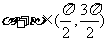 ,且
,且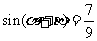 ,
,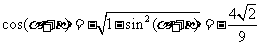 ……10分
……10分
故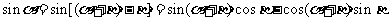 ……………………………12分
……………………………12分
=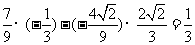 ………………………………………………………………………14分
………………………………………………………………………14分
6.解:⑴由
所以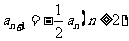
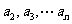 成等比……………3分
成等比……………3分
故 …………4分
…………4分
⑵依题意: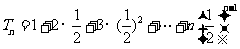
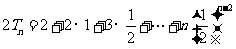
两式错们相减得: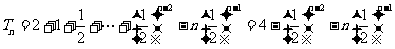
所以对一切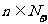 有
有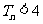 且
且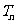 是递增的
是递增的
又因为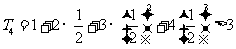
所以满足条件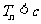 的最小正整数
的最小正整数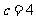 …………8分
…………8分
⑶记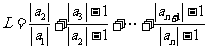
一方面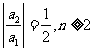 时
时
所以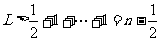 …………10分
…………10分
另一方面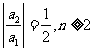 时
时
 (只有
(只有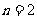 时取等)
时取等)
所以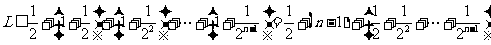
= …………12分
…………12分
5.解⑴因为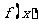 是二次函数,且
是二次函数,且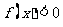 的解集是
的解集是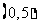
所以可设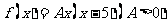
所以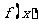 在区间
在区间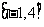 上最大值是
上最大值是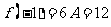 所以
所以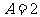 所以
所以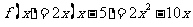 ………………6分
………………6分
⑵由已知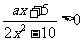 所以
所以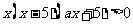 又
又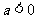
所以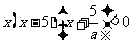 ………………8分
………………8分
①
若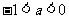 ,则
,则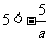 所以
所以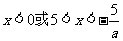
②
若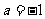 ,则
,则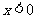
③
若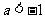 ,则
,则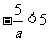 ,所以
,所以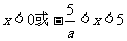 ………………11分
………………11分
综上知:当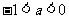 时,原不等式的解集为
时,原不等式的解集为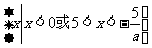
当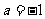 时,原不等式的解集为
时,原不等式的解集为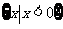
当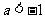 时,原不等式的解集为
时,原不等式的解集为 ……………12分
……………12分
4.因为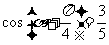
所以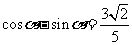 ………2分
………2分
平方得: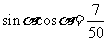 …………5分
…………5分
⑵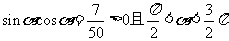 所以
所以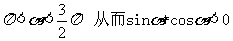
又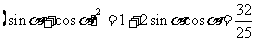
所以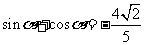 又
又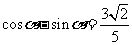
所以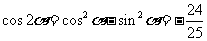 ……………………9分
……………………9分
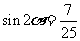 ………10分
………10分
故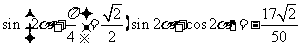 ……………12分
……………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com