
题目列表(包括答案和解析)
9. 解:①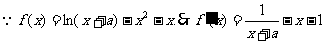
又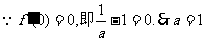 ………4分
………4分
由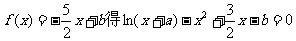 k+s-5#u
k+s-5#u

设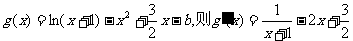
即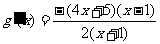

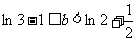 …………12分k+s-5#u
…………12分k+s-5#u

8.解:(1)∵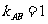 ,AB的中点坐标为(1,2)
,AB的中点坐标为(1,2)
∴直线CD的方程为: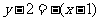 即
即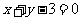 .……3分
.……3分
(2)设圆心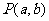 ,则由P在CD上得
,则由P在CD上得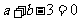 .……4分
.……4分
又直径|CD|=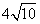 ,∴|PA|=
,∴|PA|=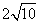
∴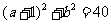 . k+s-5#u
. k+s-5#u 
①代入②消去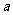 得
得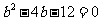 ,
,
解得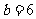 或
或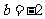
当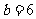 时
时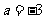 ,当
,当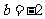 时
时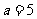
∴圆心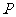 (-3,6)或
(-3,6)或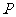 (5,-2)
(5,-2)
∴圆P的方程为:
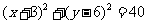 或
或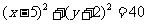 ----------------8分
----------------8分
k+s-5#u

(3)
∵|AB|=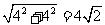 .
.
∴当△QAB面积为8时,点Q到直线AB的距离为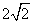
又圆心到直线AB的距离为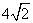 ,圆P的半径
,圆P的半径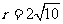 ,且
,且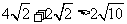
∴圆上共有两个点Q,使△QAB的面积为8. .…… 12分
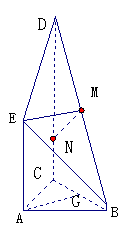
7. 解:由题意,Ea⊥平面ABC , DC⊥平面ABC ,AE∥DC,ae=2, dc=4 ,ab⊥ac,

 且AB=AC=2
且AB=AC=2
 (1)∵Ea⊥平面ABC,∴ea⊥ab, 又ab⊥ac,
(1)∵Ea⊥平面ABC,∴ea⊥ab, 又ab⊥ac,
 ∴ab⊥平面acde ,
2分
∴ab⊥平面acde ,
2分
 ∴四棱锥b-acde的高h=ab=2,梯形acde的面积S= 6
∴四棱锥b-acde的高h=ab=2,梯形acde的面积S= 6

 ∴
∴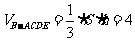 ,
即所求几何体的体积为4…………………4分
,
即所求几何体的体积为4…………………4分
 (2)证明:∵m为db的中点,取bc中点G,连接em,mG,aG,
(2)证明:∵m为db的中点,取bc中点G,连接em,mG,aG,

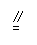 ∴ mG∥DC,且
∴ mG∥DC,且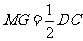
 ∴ mG
ae,∴四边形aGme为平行四边形,
6分
∴ mG
ae,∴四边形aGme为平行四边形,
6分
 ∴em∥aG, 又AG
∴em∥aG, 又AG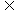 平面ABC ∴EM∥平面ABC.……8分
平面ABC ∴EM∥平面ABC.……8分
 (3)由(2)知,em∥aG,
(3)由(2)知,em∥aG,
 又∵平面BCD⊥底面ABC,aG⊥bc,∴AG⊥平面BCD
又∵平面BCD⊥底面ABC,aG⊥bc,∴AG⊥平面BCD
 ∴EM⊥平面BCD,又∵EM
∴EM⊥平面BCD,又∵EM 平面BDE,
平面BDE,
 ∴平面BDE⊥平面BCD
k+s-5#u
∴平面BDE⊥平面BCD
k+s-5#u 
 在平面BCD中,过M作MN⊥DB交DC于点N,
在平面BCD中,过M作MN⊥DB交DC于点N,
 ∴MN⊥平面BDE
点n即为所求的点
.……10分
∴MN⊥平面BDE
点n即为所求的点
.……10分

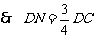 ∵
∵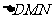 ∽
∽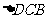
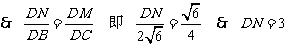

 ∴ 边DC上存在点N,满足DN=
∴ 边DC上存在点N,满足DN=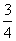 DC时,有NM⊥平面BDE. .…… 12分
DC时,有NM⊥平面BDE. .…… 12分
6.解依题: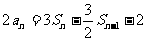 ,
, …2分
…2分
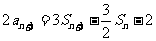
做差得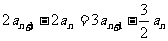

得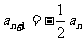
 …4分
…4分
又因为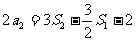 k+s-5#u
k+s-5#u 
解得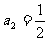 …6分
…6分
故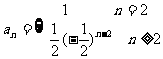 …9分
…9分
故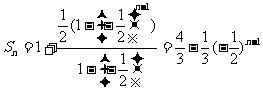 …12分
…12分
5.(1)由8x f(x)
f(x) 4(x2+1),∴f(1)=8,f(-1)=0,∴b=4
4(x2+1),∴f(1)=8,f(-1)=0,∴b=4
又8x f(x)
f(x) 4(x2+1) 对
4(x2+1) 对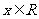 恒成立,∴a=c=2 f(x)=2(x+1)2 k+s-5#u
恒成立,∴a=c=2 f(x)=2(x+1)2 k+s-5#u 
(2)∵g(x)=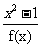 =
=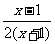 ,D={x︱x
,D={x︱x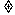 -1 }
-1 }
X1=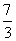 ,x2=
,x2=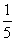 ,x3=-
,x3=-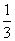 ,x4=-1,∴M={
,x4=-1,∴M={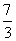 ,
,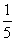 ,-
,-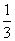 ,-1}
,-1}

4. (1)当x∈[-1,0)时, f(x)= f(-x)=loga[2-(-x)]=loga(2+x).
当x∈[2k-1,2k),(k∈Z)时,x-2k∈[-1,0], f(x)=f(x-2k)=loga[2+(x-2k)].
当x∈[2k,2k+1](k∈Z)时,x-2k∈[0,1], f(x)=f(x-2k)=loga[2-(x-2k)].
故当x∈[2k-1,2k+1](k∈Z)时, f(x)的表达式为
|
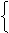 loga[2+(x-2k)],x∈[2k-1,2k),
loga[2+(x-2k)],x∈[2k-1,2k),
loga[2-(x-2k)],x∈[2k,2k+1].
(2)∵f(x)是以2为周期的周期函数,且为偶函数,∴f(x)的最大值就是当x∈[0,1]时f(x)的最大值,∵a>1,∴f(x)=loga(2-x)在[0,1]上是减函数,
∴[f(x)]max= f(0)=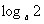 =
=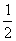 ,∴a=4. k+s-5#u
,∴a=4. k+s-5#u 
当x∈[-1,1]时,由f(x)>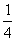 得
得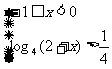

或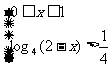 得
得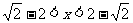
∵f(x)是以2为周期的周期函数,
∴f(x)>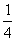 的解集为{x|2k+
的解集为{x|2k+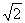 -2<x<2k+2-
-2<x<2k+2-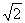 ,k∈Z
,k∈Z
3.(I)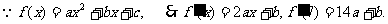 ……1分
……1分
根据题意, …………4分
…………4分
解得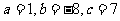 . …………7分
. …………7分
(II)因为 ……7分
……7分
(i) 时,函数
时,函数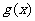 无最大值,
无最大值,
不合题意,舍去. …………11分
(ii)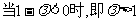 时,根据题意得
时,根据题意得 
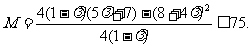
解之得 …………13分
…………13分
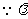 为正整数,
为正整数,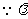 =3或4. …………14分
=3或4. …………14分
2.(1)当0<t≤10时,
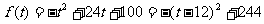 是增函数,且f(10)=240
是增函数,且f(10)=240
当20<t≤40时,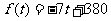 是减函数,且f(20)=240 所以,讲课开始10分钟,学生的注意力最集中,能持续10分钟。(3)当0<t≤10时,令
是减函数,且f(20)=240 所以,讲课开始10分钟,学生的注意力最集中,能持续10分钟。(3)当0<t≤10时,令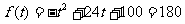 ,则t=4 当20<t≤40时,令
,则t=4 当20<t≤40时,令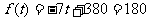 ,则t≈28.57
,则t≈28.57
则学生注意力在180以上所持续的时间28.57-4=24.57>24
从而教师可以第4分钟至第28.57分钟这个时间段内将题讲完。 
1.(1)由题意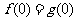 ,
,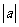 =1又a>0,所以a=1.
=1又a>0,所以a=1.
(2)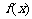
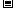 g(x)=
g(x)=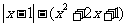 ,当
,当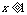 时,
时,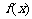
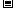
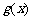 =
=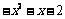 ,无递增区间;当x<1时,
,无递增区间;当x<1时,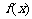
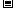
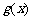 =
=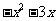 ,它的递增区间是
,它的递增区间是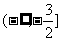 .
.
综上知: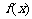
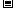
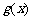 的单调递增区间是
的单调递增区间是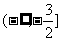 .
. 
10.(12分)设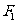 、
、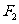 分别是椭圆
分别是椭圆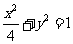 的左、右焦点.
的左、右焦点.
(1)若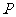 是第一象限内该椭圆上的一点,且
是第一象限内该椭圆上的一点,且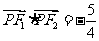 ,求点
,求点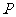 的作标;
的作标;
(2)设过定点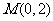 的直线
的直线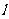 与椭圆交于同的两点
与椭圆交于同的两点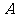 、
、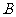 ,且
,且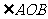 为锐角(其中
为锐角(其中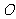 为作标原点),求直线
为作标原点),求直线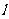 的斜率
的斜率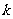 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com