
题目列表(包括答案和解析)
1 判断下列函数的奇偶性
判断下列函数的奇偶性
(1)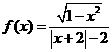 (2)
(2)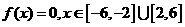
2 已知函数
已知函数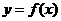 的定义域为
的定义域为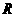 ,且对任意
,且对任意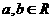 ,都有
,都有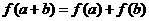 ,且当
,且当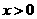 时,
时,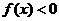 恒成立,证明:(1)函数
恒成立,证明:(1)函数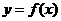 是
是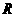 上的减函数;
上的减函数;
(2)函数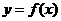 是奇函数
是奇函数
3 设函数
设函数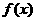 与
与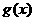 的定义域是
的定义域是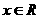 且
且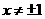 ,
,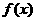 是偶函数,
是偶函数, 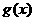 是奇函数,且
是奇函数,且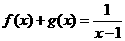 ,求
,求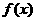 和
和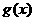 的解析式
的解析式
4 设
设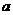 为实数,函数
为实数,函数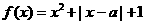 ,
,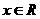
(1)讨论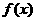 的奇偶性;
的奇偶性;
(2)求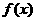 的最小值
的最小值
1 函数
函数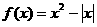 的单调递减区间是____________________
的单调递减区间是____________________
2 已知定义在
已知定义在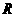 上的奇函数
上的奇函数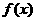 ,当
,当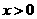 时,
时, ,
,
那么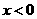 时,
时,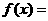

3 若函数
若函数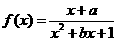 在
在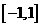 上是奇函数,则
上是奇函数,则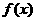 的解析式为________
的解析式为________
4 奇函数
奇函数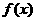 在区间
在区间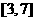 上是增函数,在区间
上是增函数,在区间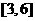 上的最大值为
上的最大值为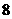 ,
,
最小值为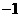 ,则
,则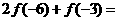 __________
__________
5 若函数
若函数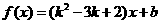 在
在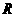 上是减函数,则
上是减函数,则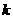 的取值范围为__________
的取值范围为__________
1 下列判断正确的是( )
下列判断正确的是( )
A 函数
函数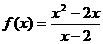 是奇函数
B
是奇函数
B 函数
函数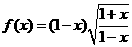 是偶函数
是偶函数
C 函数
函数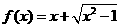 是非奇非偶函数 D
是非奇非偶函数 D 函数
函数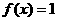 既是奇函数又是偶函数
既是奇函数又是偶函数
2 若函数
若函数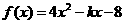 在
在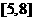 上是单调函数,则
上是单调函数,则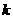 的取值范围是( )
的取值范围是( )
A
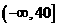 B
B
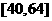
C
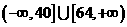 D
D
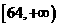
3 函数
函数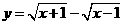 的值域为( )
的值域为( )
A
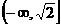 B
B
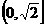
C
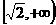 D
D
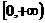
4 已知函数
已知函数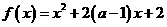 在区间
在区间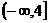 上是减函数,
上是减函数,
则实数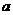 的取值范围是( )
的取值范围是( )
A
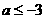 B
B
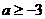 C
C
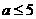 D
D
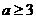
5 下列四个命题:(1)函数
下列四个命题:(1)函数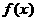 在
在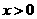 时是增函数,
时是增函数,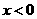 也是增函数,所以
也是增函数,所以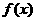 是增函数;(2)若函数
是增函数;(2)若函数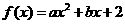 与
与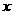 轴没有交点,则
轴没有交点,则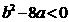 且
且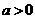 ;(3)
;(3) 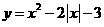 的递增区间为
的递增区间为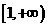 ;(4)
;(4) 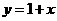 和
和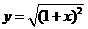 表示相等函数
表示相等函数
其中正确命题的个数是( )
A
 B
B
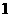 C
C
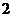 D
D
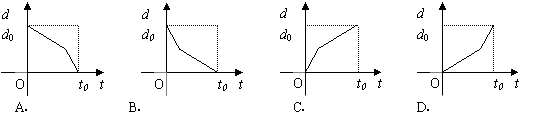 6
6 某学生离家去学校,由于怕迟到,所以一开始就跑步,等跑累了再走余下的路程
某学生离家去学校,由于怕迟到,所以一开始就跑步,等跑累了再走余下的路程 在下图中纵轴表示离学校的距离,横轴表示出发后的时间,则下图中的四个图形中较符合该学生走法的是( )
在下图中纵轴表示离学校的距离,横轴表示出发后的时间,则下图中的四个图形中较符合该学生走法的是( )
1 求函数
求函数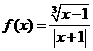 的定义域
的定义域
2 求函数
求函数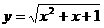 的值域
的值域
3
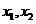 是关于
是关于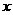 的一元二次方程
的一元二次方程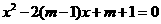 的两个实根,又
的两个实根,又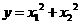 ,
,
求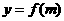 的解析式及此函数的定义域
的解析式及此函数的定义域
4 已知函数
已知函数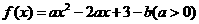 在
在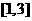 有最大值
有最大值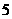 和最小值
和最小值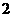 ,求
,求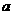 、
、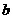 的值
的值
1 设函数
设函数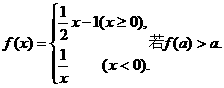 则实数
则实数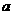 的取值范围是
的取值范围是

2 函数
函数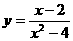 的定义域
的定义域

3 若二次函数
若二次函数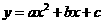 的图象与x轴交于
的图象与x轴交于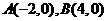 ,且函数的最大值为
,且函数的最大值为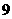 ,
,
则这个二次函数的表达式是

4 函数
函数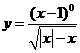 的定义域是_____________________
的定义域是_____________________
5 函数
函数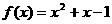 的最小值是_________________
的最小值是_________________
1 判断下列各组中的两个函数是同一函数的为( )
判断下列各组中的两个函数是同一函数的为( )
⑴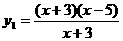 ,
,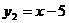 ;
;
⑵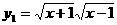 ,
,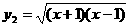 ;
;
⑶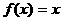 ,
,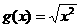 ;
;
⑷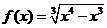 ,
,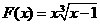 ;
;
⑸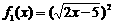 ,
,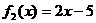

A ⑴、⑵ B
⑴、⑵ B ⑵、⑶ C
⑵、⑶ C ⑷ D
⑷ D ⑶、⑸
⑶、⑸
2 函数
函数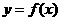 的图象与直线
的图象与直线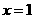 的公共点数目是( )
的公共点数目是( )
A
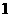 B
B
 C
C
 或
或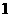 D
D
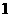 或
或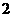
3 已知集合
已知集合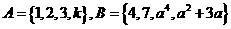 ,且
,且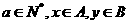
使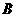 中元素
中元素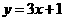 和
和 中的元素
中的元素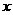 对应,则
对应,则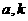 的值分别为( )
的值分别为( )
A
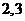 B
B
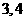 C
C
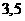 D
D
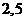
4 已知
已知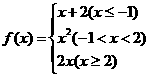 ,若
,若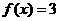 ,则
,则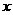 的值是( )
的值是( )
A
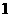 B
B
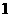 或
或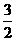 C
C
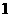 ,
,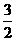 或
或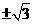 D
D
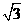
5 为了得到函数
为了得到函数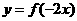 的图象,可以把函数
的图象,可以把函数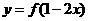 的图象适当平移,
的图象适当平移,
这个平移是( )
A 沿
沿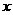 轴向右平移
轴向右平移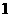 个单位 B
个单位 B 沿
沿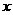 轴向右平移
轴向右平移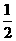 个单位
个单位
C 沿
沿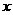 轴向左平移
轴向左平移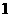 个单位 D
个单位 D 沿
沿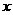 轴向左平移
轴向左平移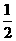 个单位
个单位
6 设
设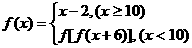 则
则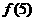 的值为( )
的值为( )
A
 B
B
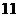 C
C
 D
D
15. 如图,设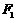 、
、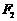 分别为椭圆
分别为椭圆 :
: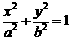 (
(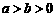 )的左、右焦点.
)的左、右焦点.
(1)设椭圆C上的点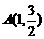 到F1、F2两点距离之和等于4,求椭圆C的方程和离心率;
到F1、F2两点距离之和等于4,求椭圆C的方程和离心率;
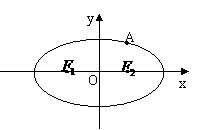 (2)设点K是(1)中所得椭圆上的动点,求线段
(2)设点K是(1)中所得椭圆上的动点,求线段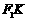 的中点的轨迹方程.
的中点的轨迹方程.
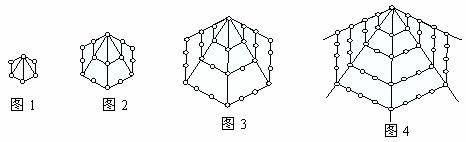
14. 在一次珠宝展览会上,某商家展出一套珠宝首饰,第一件首饰是1颗珠宝, 第二件首饰是由6颗珠宝(图中圆圈表示珠宝)构成如图1所示的正六边形, 第三件首饰如图2, 第四件首饰如图3, 第五件首饰如图4, 以后每件首饰都在前一件上,按照这种规律增加一定数量的珠宝,使它构成更大的正六变形,依此推断第6件首饰上应有_______________颗珠宝,第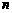 件首饰所用珠宝总数为_________________颗.
件首饰所用珠宝总数为_________________颗.
13. 直线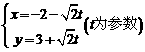 上与点
上与点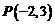 距离等于
距离等于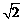 的点的坐标是
.
的点的坐标是
.
12.(文)已知椭圆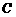 以坐标原点为中心,坐标轴为对称轴,且椭圆
以坐标原点为中心,坐标轴为对称轴,且椭圆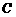 以抛物线
以抛物线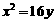 的焦点为焦点,以双曲线
的焦点为焦点,以双曲线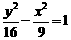 的焦点为顶点,则椭圆
的焦点为顶点,则椭圆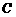 的标准方程为______________________.
的标准方程为______________________.
(理)二项式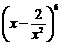 展开式中常数项为_________________.(结果用数字表示).
展开式中常数项为_________________.(结果用数字表示).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com