20．(本小题14分)(2009·太原模拟)已知数列{a_n}的前n项和S_n＝(a_n－1)(a为常数，且a≠0，a≠1，n∈N^*)，数列{b_n}满足b₁+2b₂+…+(n－1)b_n－1+nb_n＝yz{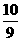}^n-1 -.

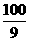(1)求a_n与b_n的表达式；

(2)设c_n＝(n+)bn，试问数列{c_n}有没有最小项？如果有，求出这个最小项；如果没有，请说明理由．

解析：(1)因为S_n＝(a_n－1)，

所以，当n＝1时，a₁＝S₁＝(a₁－1)，解之得a₁＝a；

当n≥2时，a_n＝S_n－S_n－1＝a_n－a_n－1，即＝a.

又a≠0，a≠1，所以数列{a_n}是等比数列．

所以a_n＝a·a^n－1＝aⁿ.

由b₁+2b₂+…+(n－1)b_n－1+nb_n＝(n+10)·()^n－1－得：b₁+2b₂+…+(n－1)b_n－1＝(n+9)·()^n－2－(n≥2)．

两式相减得nb_n＝(n+10)·()^n－1－(n+9)·()^n－2＝－()^n－2.

故b_n＝－·()^n－1(n≥2)，

当n＝1时，b₁＝11－＝－也符合上式，

故b_n＝－·()^n－1.

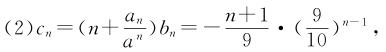
所以c_n+1－c_n＝－()ⁿ+()^n－1

＝·()^n－1.

当n＞8时，c_n+1＞c_n，故c₉＜c₁₀＜…，

当n＝8时，c_n+1－c_n＝0，故c₉＝c₈，

当n＜8时，c_n+1＜c_n，故c₁＞c₂＞c₃＞…＞c₈.

综上可得，c₉、c₈是数列的最小项且c₈＝c₉＝－()⁷.

19．(本小题12分)已知函数f(x)＝ln(2+3x)+x²在x＝处取得极值．

(1)求f(x)在[0,1]上的单调区间；

(2)若对任意的x∈[，]，不等式|a－lnx|+ln[f′(x)+3x]＞0恒成立，求实数a的取值范围．

解析：(1)由题意得函数f(x)的定义域为{x|x＞－}，

f′(x)＝+mx＝，

又函数f(x)在x＝处取得极值，

∴f′()＝0，即m＝－3，

此时，f′(x)＝.

∴在[0,1]上，当0≤x＜时，f′(x)＞0，函数f(x)单调递增；当＜x≤1，f′(x)＜0，函数f(x)单调递减．∴f(x)在x＝处取得极大值．

∴f(x)在[0,1]上的单调递增区间为[0，]，单调递减区间为[，1]．

(2)∵f′(x)+3x＝，

∴当x∈[，]时，ln[f′(x)+3x]∈[0，ln](当且仅当x＝时，ln[f′(x)+3x]＝0)．

因此，不等式|a－lnx|+ln[f′(x)+3x]＞0恒成立的a的取值范围是(－∞，ln)∪(ln，+∞)．

18．(本小题12分)如图，在棱长为2的正方体ABCD－A₁B₁C₁D₁中，E、F、M、H分别为A₁D₁、CC₁、AB、DB₁的中点．

(1)求证：EF∥平面ACD₁；

(2)求证：MH⊥B₁C；

(3)在棱BB₁上是否存在一点P，使得二面角P－AC－B的大小为30°？若存在，求出BP的长；若不存在，请说明理由．

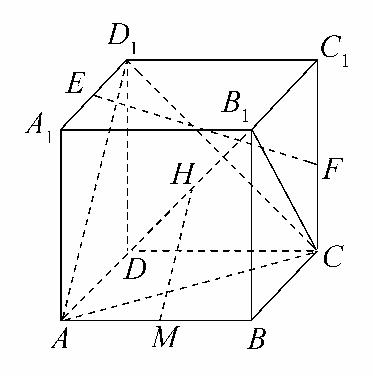
解析：(1)取AA₁的中点G，连接GF，则GF∥AC，

连接GE，则GE∥AD₁，∴平面ACD₁∥平面GFE.

又∵EF⊂平面GFE，∴EF∥平面ACD₁.

(2)连接AC₁，∵H为DB₁的中点，

∴H为AC₁的中点，连接BC₁，设BC₁交B₁C于点O，

∵M为AB的中点，

∴MH∥BC₁.

在正方形BCC₁B₁中，BC₁⊥B₁C，

∴MH⊥B₁C.

(3)如图，

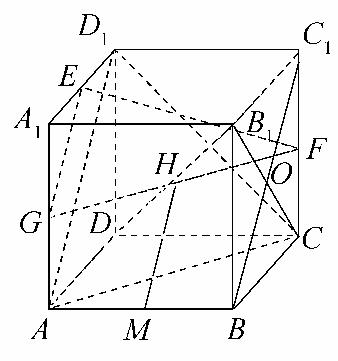
分别以DA、DC、DD₁所在的直线为x轴、y轴、z轴建立空间直角坐标系D－xyz，则由已知得D(0,0,0)，A(2,0,0)，B(2,2,0)，C(0,2,0)，B₁(2,2,2)．

设点P(2,2，t)(0＜t≤2)，平面ACP的一个法向量为n＝(x，y，z)，则

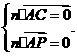
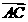∵＝(－2,2,0)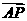，＝(0,2，t)，

∴，取n＝(1,1，－)．

易知平面ABC的一个法向量为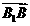＝(0,0,2)，

假设P点存在，使得二面角P－AC－B的大小为θ＝30°，

则cosθ＝|cos〈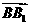，n〉|＝＝，

即＝(2+)，解得t＝.

∴∈(0,2]，∴在棱BB₁上存在一点P，当BP的长为时，二面角P－AC－B的大小为30°.

17．(本小题12分)在一个盒子中，放有标号分别为1,2,3的三张卡片，现从这个盒子中有放回地先后抽取两张卡片，并设它们的标号分别为x，y，记ξ＝|x－2|+|y－x|.

(1)求随机变量ξ的最大值，并求事件“ξ取得最大值”的概率；

(2)求随机变量ξ的分布列和数学期望．

解析：(1)∵x、y可能的取值分别为1、2、3，∴|x－2|≤1，|y－x|≤2，∴ξ≤3，且当x＝1，y＝3或x＝3，y＝1时，ξ＝3.因此，随机变量ξ的最大值为3.

∵有放回地先后抽取两张卡片共有3×3＝9种不同的情况，

∴P(ξ＝2)＝.

(2)ξ的所有可能的取值为0,1,2,3.∵ξ＝0时，只有x＝2，y＝2这一种情况，

ξ＝1时，x＝1，y＝1或x＝2，y＝1或x＝2，y＝3或x＝3，y＝3四种情况．

ξ＝2时，有x＝1，y＝2或x＝3，y＝2两种情况．

∴P(ξ＝0)＝，P(ξ＝1)＝，P(ξ＝2)＝，

∴随机变量ξ的分布列为：

因此，数学期望Eξ＝0×+1×+2×+3×＝.

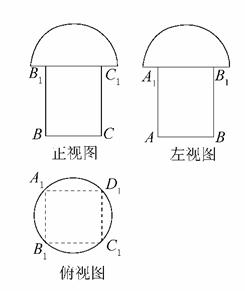
16．如图为一个几何体的三视图，AB＝BC＝1，BB₁＝2，则此几何体的表面积为__________．

解析：

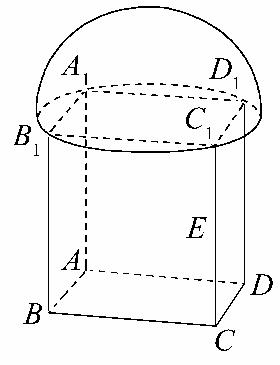
此几何体是由一个半球和一个长方体组合而成的，故其直观图如图所示．

因为AB＝BC＝1，故B₁D₁＝，故半球的半径R＝，因此半球的表面积S_半球表＝×4πR²+πR²＝.

长方体的表面积S_长方体表＝4×1×2+2＝10，长方体的上底面的面积S_{长方体上底面}＝1，故此几何体的表面积S_表＝S_半球表+S_长方体表－2S_{长方体上底面}＝+8.

答案：+8

15．已知数列{a_n}的通项公式a_n＝，计算其前102项和的算法流程图如图所示，图中①，②应该填__________、__________.

解析：算法流程图中用的循环体中应有使循环结束的语句，故应有n＝cdefghijklm1使原来的n的值增加1，故应在求和后，所以应填在②中，而①应填给a_n赋值的语句a_n＝a_n－4.

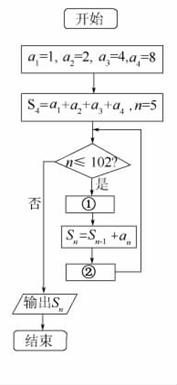
答案：a_n＝a_n－4　n＝n+1

14．已知α，β∈(－，)，且tanα，tanβ是方程x²+3x+4＝0的两个根，则α+β＝__________.

解析：依题意得tanα+tanβ＝－3＜0，tanα·tanβ＝4＞0，∴tan(α+β)＝＝＝.易知tanα＜0，tanβ＜0，又α，β∈(－，)，∴α∈(－，0)，β∈(－，0)，∴α+β∈(－π，0)，∴α+β＝－.

答案：－

13．已知在区间(a，b)上，f(x)＞0，f′(x)＞0，对x轴上的任意两点(x_1,0)，(x_2,0)，(a＜x₁＜x₂＜b)都有f()＞.若S₁＝f(x)dx，S₂＝(b－a)，S₃＝f(a)(b－a)，则S₁、S₂、S₃的大小关系为__________．

解析：根据定积分的几何意义知S₁为f(x)的图象与直线x＝a，x＝b及x轴围成的曲边梯形的面积，而s₂为梯形的面积，s₃为矩形的面积，所以结合题意并画出图形可得S₁＞S₂＞S₃.

答案：S₁＞S₂＞S₃

12．已知a＞0且a≠1，f(x)＝x²－a^x，当x∈(－1,1)时均有f(x)＜，则实数a的取值范围是(　)

A．(0，]∪[2，+∞)　 　　　　　　 B．[，1)∪(1,4]

C．[，1)∪(1,2]　 　　　　　　　　　　 D．(0，]∪[4，+∞)

解析：f(x)＜即x²－a^x＜，x²－＜a^x.当0＜a＜1时，如图甲所示，在x＝1处，得≤a，∴≤a＜1；当a＞1时，如图乙所示，在x＝－1处，得≤，∴1＜a≤2.

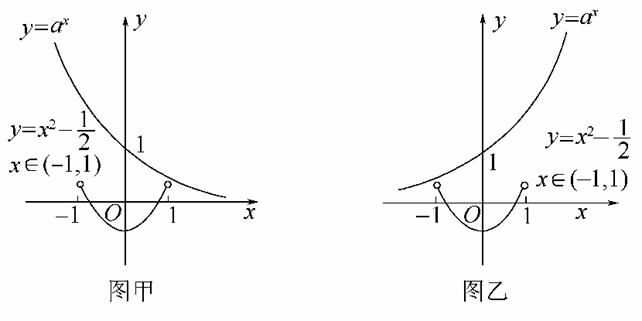
答案：C

11．当不等式组所表示的平面区域的面积最小时，实数k的值为(　)

A．－　 B．－　 C．－1　 D．－2

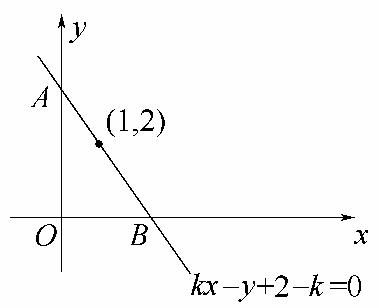
解析：不等式组所表示的平面区域由三条直线围成，其中直线kx－y+2－k＝0(k＜0)即y－2＝k(x－1)(k＜0)经过定点(1,2)，因此问题转化为求经过定点(1,2)的直线与两坐标轴在第一象限内所围成的三角形的面积的最小值．如图所示，设所围成的区域的面积为S，则S＝·|OA|·|OB|＝·|2－k|·|1－|.

因为k＜0，所以－k＞0，所以S＝(4－k－)＝[4+(－k)+(－)]≥[4+2 ]＝4，

当S取得最小值4时，－k＝－，解得k＝－2.

答案：D