
题目列表(包括答案和解析)
5、在一条公路上每隔10公里有一个仓库,共有5个仓库。一号仓库
存有则10吨货物,二号仓库存有20吨货物,五号仓库存有40吨
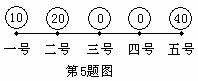 货物,其余两个仓库是空的。现在要把所有的货物集中
货物,其余两个仓库是空的。现在要把所有的货物集中
存放一个仓库里,若每吨货物运输1公里需要0.5元运
输费,则最少需要的运费是( )
A、450元 B、500元
C、550元 D、600元
4、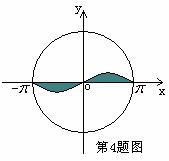 如图,圆
如图,圆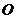 :
: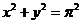 内的正弦曲线
内的正弦曲线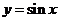 与
与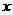 轴围成的区域记为
轴围成的区域记为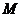 (图中阴影部分),随机往圆
(图中阴影部分),随机往圆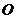 内投一个点
内投一个点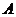 ,则点
,则点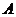 落在区域
落在区域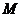 内的概率是( )
内的概率是( )
A、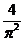 B、
B、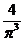
C、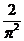 D、
D、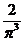
3、已知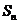 为等差数列
为等差数列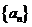 的前
的前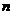 项和,若
项和,若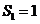 ,
,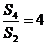 ,则
,则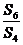 的值为( )
的值为( )
A、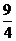 B、
B、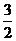 C、
C、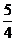 D、4
D、4
2、已知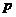 :“
:“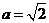 ”,
”,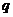 :“直线
:“直线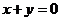 与圆
与圆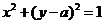 相切”,则
相切”,则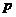 是
是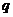 的( )
的( )
A、充分非必要条件 B、必要非充分条件
C、充要条件 D、既非充分也非必要条件
项中,只有一项是符合题目要求的。
1、已知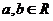 ,若
,若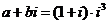 (其中
(其中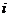 为虚数单位),则( )
为虚数单位),则( )
A、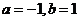 B、
B、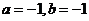 C、
C、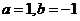 D、
D、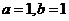
24.(本小题满分10分)选修4-5:不等式选讲
设函数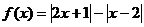 .
.
(Ⅰ)求不等式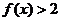 的解集;
的解集;
(Ⅱ)若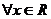 ,
,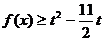 恒成立,求实数
恒成立,求实数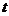 的取值范围.
的取值范围.
23.(本小题满分10分)选修4-4:坐标系与参数方程
已知在直角坐标系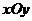 中,圆锥曲线
中,圆锥曲线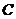 的参数方程为
的参数方程为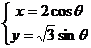 (
(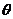 为参数),定点
为参数),定点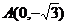 ,
,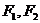 是圆锥曲线
是圆锥曲线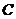 的左,右焦点.
的左,右焦点.
(Ⅰ)以原点为极点、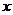 轴正半轴为极轴建立极坐标系,求经过点
轴正半轴为极轴建立极坐标系,求经过点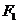 且平行于直线
且平行于直线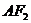 的直线
的直线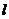 的极坐标方程;
的极坐标方程;
(Ⅱ)在(I)的条件下,设直线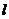 与圆锥曲线
与圆锥曲线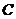 交于
交于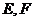 两点,求弦
两点,求弦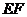 的长.
的长.
22.(本小题满分10分)选修4-1:几何证明选讲
如图,直线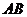 经过⊙
经过⊙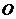 上的点
上的点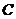 ,并且
,并且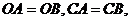 ⊙
⊙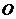 交直线
交直线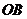 于
于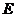 ,
,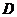 ,连接
,连接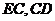 .
.
(Ⅰ)求证:直线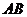 是⊙
是⊙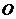 的切线;
的切线;
(Ⅱ)若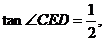 ⊙
⊙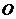 的半径为
的半径为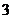 ,求
,求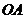 的长.
的长.
21.(本小题满分12分)
已知函数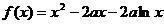 (
(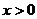 ,
,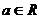 ),
),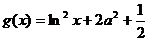 .
.
(Ⅰ)证明:当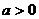 时,对于任意不相等的两个正实数
时,对于任意不相等的两个正实数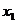 、
、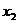 ,均有
,均有
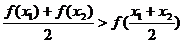 成立;
成立;
(Ⅱ)记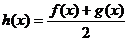 ,
,
(ⅰ)若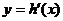 在
在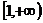 上单调递增,求实数
上单调递增,求实数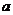 的取值范围;
的取值范围;
(ⅱ)证明: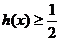 .
.
请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.
20.(本小题满分12分)
已知椭圆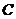 :
: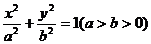 ,
,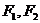 分别为左,右焦点,离心率为
分别为左,右焦点,离心率为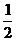 ,点
,点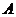 在椭圆
在椭圆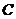 上,
上,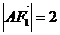 ,
,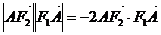 ,过
,过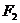 与坐标轴不垂直的直线
与坐标轴不垂直的直线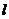 交椭圆于
交椭圆于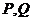 两点.
两点.
(Ⅰ)求椭圆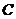 的方程;
的方程;
(Ⅱ)在线段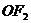 上是否存在点
上是否存在点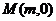 ,使得以线段
,使得以线段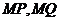 为邻边的四边形是菱形?若存在,求出实数
为邻边的四边形是菱形?若存在,求出实数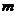 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com