5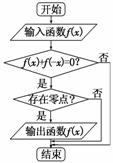．(2011·江南十校)某流程图如图所示，现输入如下四个函数，则可以输出的函数是(　)

A．f(x)＝x²

B．f(x)＝

C．f(x)＝

D．f(x)＝

解析：根据流程图可知输出的函数为奇函数，并且存在零点．经验证：选项A，f(x)＝x²为偶函数；选项B，f(x)＝不存在零点；选项C，f(x)的定义域为全体实数，f(－x)＝＝－f(x)，因此为奇函数，并且由f(x)＝＝0可得x＝0，存在零点；选项D，f(x)＝不具有奇偶性．

答案：C

4．有编号为1,2，…，700的产品，现需从中抽取所有编号能被7整除的产品作为样品进行检验．下面是四位同学设计的程序框图，其中正确的是(　)

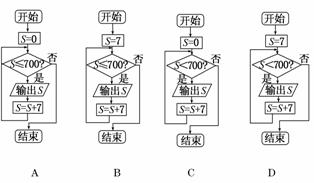
解析：选项A、C中的程序框图会输出0，故排除A、C；选项D中的程序框图不能输出700，故排除D.

答案：B

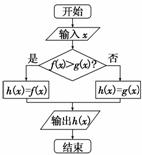
3．在如图所示的算法流程图中，若f(x)＝2^x，g(x)＝x³，则h(2)的值为(　)

A．9　 　　　　　　　　　　　　　　　　　　　　 B．8

C．6　 　　　　　　　　　　　　　　　　　　　　 D．4

解析：当x＝2时，f(x)＝4，g(x)＝8，此时f(x)<g(x)，于是h(x)＝g(x)＝g(2)＝8.

答案：B

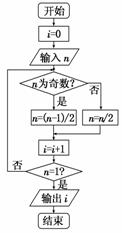
2．在如图的程序框图中，输入n＝60，按程序运行后输出的结果是(　)

A．0 　　　　　　　　　　 　B．3

C．4 　　　　　　　　　　 　D．5

解析：根据程序框图可知，输出的结果是循环的次数．经过执行5次循环后n＝1，所以输出的结果i＝5.

答案：D

1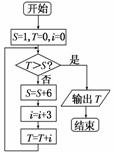．执行如图所示的程序框图，则输出的结果为(　)

A．20　　　　　B．30

C．40 　 　　　　　　　　　　　 D．50

解析：按照程序框图依次执行为S＝7，i＝3，T＝3；S＝13，i＝6，T＝3+6＝9；S＝19，i＝9，T＝9+9＝18；S＝25，i＝12，T＝18+12＝30.故最后输出T＝30.

答案：B

7．中国乒乓球队甲、乙两名队员参加奥运会乒乓球女子单打比赛，甲夺得冠军的概率为，乙夺得冠军的概率为，那么中国队夺得女子乒乓球单打冠军的概率为________．

解析：设事件A为“甲夺得冠军”，事件B为“乙夺得冠军”，则P(A)＝，P(B)＝，因为事件A和事件B是互斥事件．

∴P(A∪B)＝P(A)+P(B)＝+＝.

6．设a是甲抛掷一枚骰子得到的点数，则方程x²+ax+2＝0有两个不相等的实数根的概率为(　)

A.　 　　　　　　　 B.

C.　 　　　　　　　 D.

解析：由方程x²+ax+2＝0有两个不相等的实数根，得Δ＝a²－8>0，故a＝3,4,5,6.根据古典概型的概率计算公式有P＝＝.

答案：A

5．口袋中有100个大小相同的红球、白球、黑球，其中红球45个，从口袋中摸出一个球，摸出白球的概率为0.23，则摸出黑球的概率为(　)

A．0.45　 　　　　　　　 B．0.67

C．0.64　 　　　　　　　 D．0.32

解析：P＝1－0.45－0.23＝0.32.

答案：D

4．(2011·金华十校联考)在一个袋子中装有分别标注1,2,3,4,5的5个小球，这些小球除标注的数字外完全相同，现从中随机取出2个小球，则取出小球标注的数字之差的绝对值为2或4的概率是(　)

A.　 　　　　　　 B.

C. 　　 　　　　　　　　 D.

解析：取2个小球的不同取法有(1,2)，(1,3)，(1,4)，(1,5)，(2,3)，(2,4)，(2,5)，(3,4)，(3,5)，(4,5)，共十种，其中标注的数字之差的绝对值为2或4的有(1,3)，(2,4)，(3,5)，(1,5)，共四种，故所求的概率为＝.

答案：C

3．(2011·德州模拟)一个袋子中有5个大小相同的球，其中有3个黑球与2个红球，如果从中任取两个球，则恰好取到两个同色球的概率是(　)

A. 　　　　　　　　　　　 　B.

C.　 　　　　　　　 　D.

解析：任取两球的取法有10种，取到同色球的取法有两类共有3+1＝4种，故P＝.

答案：C