
题目列表(包括答案和解析)
7.(潮州市2008~2009学年度第一学期高三级期末质量检测)
函数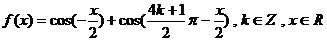 。
。
(1)求 的周期;(2)解析式及
的周期;(2)解析式及 在
在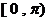 上的减区间;
上的减区间;
(3)若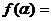
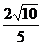 ,
,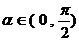 ,求
,求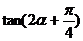 的值。
的值。
解:(1)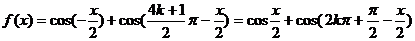
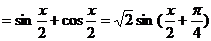 ,(
,(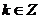 )
)
所以, 的周期
的周期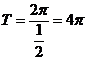 。 …… 4分
。 …… 4分
(2)由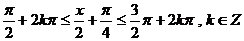 ,得
,得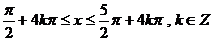 。
。
又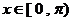 ,
,
令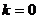 ,得
,得
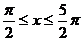 ;令
;令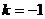 ,得
,得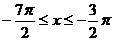 (舍去)
(舍去)
∴  在
在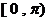 上的减区间是
上的减区间是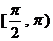 。 …… 8分
。 …… 8分
(3)由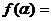
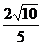 ,得
,得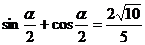 ,
,
∴ 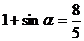 , ∴
, ∴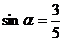
又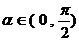 ,∴
,∴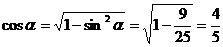
∴ 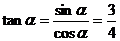 ,∴
,∴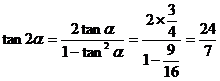
∴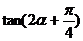
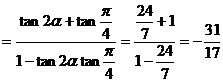 。
。
6. 已知函数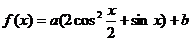 。
。
(Ⅰ)当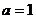 时,求
时,求 的单调递增区间:
的单调递增区间:
(Ⅱ)当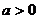 ,且
,且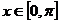 时,
时, 的值域是
的值域是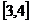 ,求
,求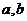 的值。
的值。
解:(Ⅰ)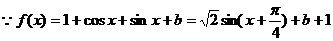 ,
,
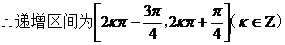
(Ⅱ)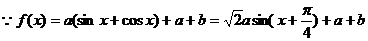

而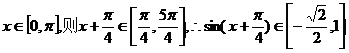
故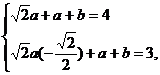
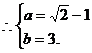
综合拔高训练
5. 已知函数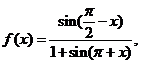
(1)求证: ;
;
(2)已知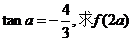 的值。
的值。
解析: f(x)= ① f(x)= =
= = = tan(+)
②f(2α)=tan(α+) = ∵tanα=- ∴f(2α) = = -
4. (深圳市外语学校2009届高三上学期第三次质量检测)
已知函数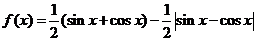 ,则
,则 的值域是
.
的值域是
.
[解析] 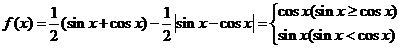
画图可得 的值域是
的值域是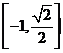
3. (深圳市外语学校2009届高三上学期第三次质量检测)
已知向量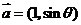 ,
,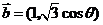 ,则
,则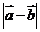 的最大值为 .
的最大值为 .
[解析]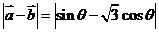 =
=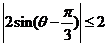 .
.
2. (华南师范附属中学2009届高三上学期第三次综合测试)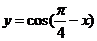 是( )上的增函数
是( )上的增函数
A.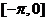 B.
B.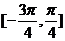 C.
C.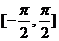 D.
D.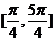
解析: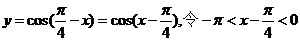 选B
选B
1. (东莞高级中学2009届高三上学期11月教学监控测试)
若函数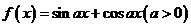 的最小正周期为1,则它的图像的一个对称中心为 ( )
的最小正周期为1,则它的图像的一个对称中心为 ( )
|
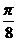 ,0) B.(0,0) C.(-
,0) B.(0,0) C.(-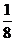 ,0) D.(
,0) D.(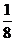 ,0)
,0)
解析: 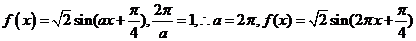 将
将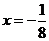 代入得函数值为0,故选C
代入得函数值为0,故选C
8. 已知函数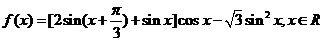
(1)求函数 的最小正周期;
的最小正周期;
(2)若存在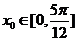 ,使不等式
,使不等式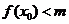 成立,求实数m的取值范围.
成立,求实数m的取值范围.
解析:(1)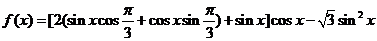
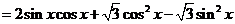
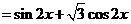

∴
函数f(x)的最小正周期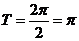
(2)当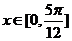 时,
时,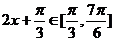
∴ 当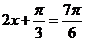 ,即
,即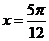 时,f(x)取最小值-1
时,f(x)取最小值-1
所以使题设成立的充要条件是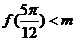 ,
,
故m的取值范围是(-1,+∞)
★抢 分 频 道
基础巩固训练
7. (汕头市金山中学2009届高三上学期11月月考)
设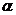 ,β都是第二象限的角,且sin
,β都是第二象限的角,且sin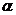 <sinβ,则()
<sinβ,则()
A.tan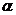 <tanβ B.cos
<tanβ B.cos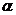 <cosβ C.tan
<cosβ C.tan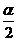 <tan
<tan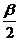 D.cos
D.cos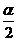 <cos
<cos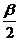
解析:取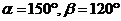 排除A,C,再取
排除A,C,再取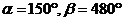 排除D,选B
排除D,选B
6. 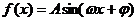 (A>0,ω>0)在x=1处取最大值,则
( )
(A>0,ω>0)在x=1处取最大值,则
( )
A、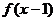 一定是奇函数 B、
一定是奇函数 B、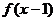 一定是偶函数
一定是偶函数
C、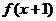 一定是奇函数 D、
一定是奇函数 D、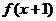 一定是偶函数
一定是偶函数
解析:D [∵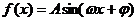 (A>0,ω>0)在x=1处取最大值∴
(A>0,ω>0)在x=1处取最大值∴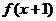 在x=0处取最大值,
即y轴是函数
在x=0处取最大值,
即y轴是函数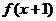 的对称轴 ∴函数
的对称轴 ∴函数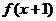 是偶函数 ]
是偶函数 ]
考点4 单调性与对称性问题
题型1.求单调区间和研究对称性
[例1](广东省六校2009届高三第二次联考试卷)已知向量 ,
, ,
,
(1)若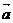 ⊥
⊥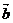 , 且-<
, 且-<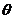 <. 求
<. 求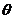 ;
;
(2)求函数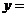 |
|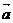 +
+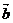 |的单调增区间和函数图像的对称轴方程.
|的单调增区间和函数图像的对称轴方程.
[解题思路]先进行向量运算,再化简三角函数式
解析(1).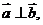
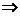
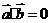
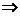
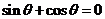
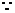 -<
-<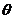 <
<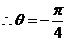
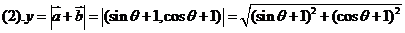
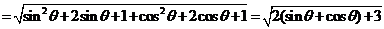

由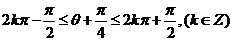 得求函数
得求函数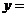 |
|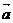 +
+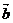 |的单调增区间是:
|的单调增区间是:
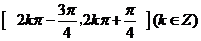
由 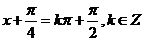 。得对称轴方程是:
。得对称轴方程是: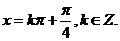
[名师指引]函数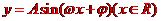 的图像有无穷多条对称轴,可由方程
的图像有无穷多条对称轴,可由方程
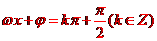 解出;它还有无穷多个对称中心,对称中心为
解出;它还有无穷多个对称中心,对称中心为
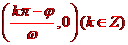 .
.
题型2.借助于单调性处理不等关系和最值问题
[例2](广雅中学08-09学年高三上学期期中考试)设向量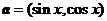 ,
,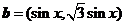 ,
,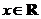 ,函数
,函数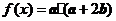 .
.
(1) 求函数 的最大值与单调递增区间;
的最大值与单调递增区间;
(2) 求使不等式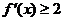 成立的
成立的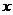 的取值集合.
的取值集合.
[解题思路]处理三角不等关系要借助于图象分析和周期性
解:(1) 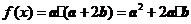

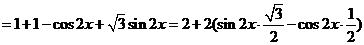
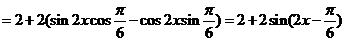 .
.
∴当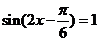 时,
时, 取得最大值
取得最大值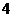 .
.
由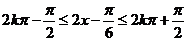 ,得
,得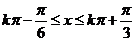
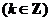 ,
,
∴ 的单调递增区间为
的单调递增区间为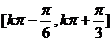
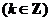 .
.
(2) 由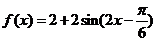 ,得
,得 .
.
由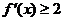 ,得
,得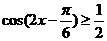 ,则
,则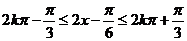 ,
,
即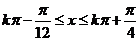
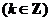 .
.
∴使不等式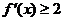 成立的
成立的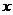 的取值集合为
的取值集合为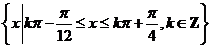 .
.
[名师指引]三角函数与导数的整合是近两年高考的一种趋势
[新题导练]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com