
题目列表(包括答案和解析)
5.( 广东省北江中学2009届高三上学期12月月考 (数学理))
“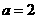 ”是“
”是“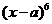 的展开式的第三项是60
的展开式的第三项是60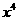 ”的________条件
(
)
”的________条件
(
)
A.充分不必要 B. 必要不充分 C. 充要 D. 既不充分也不必要
答案:A
4. (广东省深圳外国语学校2009届高三统测)
若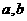 是常数, 则“
是常数, 则“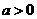 且
且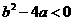 ”是“对任意
”是“对任意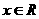 ,有
,有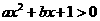 ”的 ( )
”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
答案: “对任意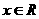 ,有
,有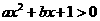 ”的等价命题是:a=0时,必有b=0;或
”的等价命题是:a=0时,必有b=0;或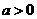 时,
时,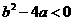 。选A
。选A
3.(广东省四会中学2009届高三质量检测)
△ABC中“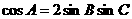 ”是“△ABC为钝角三角形”的( )
”是“△ABC为钝角三角形”的( )
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分也不必要
答案:B
2. 设原命题:若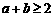 ,则
,则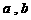 中至少有一个不小于1.
中至少有一个不小于1.
则原命题与其逆命题的真假情况是( )A
A.原命题真,逆命题假 B.原命题假,逆命题真
C.原命题与逆命题均为真命题 D.原命题与逆命题均为假命题
答案: A. 提示: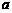 =1.2,
=1.2,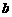 =0.3,则
=0.3,则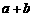 =1.5
=1.5 2,∴逆命题为假.
2,∴逆命题为假.
1. 下列语句中命题的个数是( )
① 地球是太阳系的一颗行星; ② 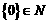 ;③ 这是一颗大树;④
;③ 这是一颗大树;④ 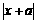 ;⑤
;⑤ 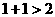 ⑥ 老年人组成一个集合;
⑥ 老年人组成一个集合;
A.1 B.2 C.3 D.4
解:①②⑤⑥是命题,故选D
11.(广东省深圳市2009 届高三九校联考)
设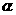 、
、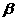 是方程
是方程 的两个实根。那么“
的两个实根。那么“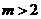 且
且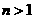 ”是“两根
”是“两根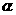 、
、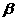 均大于
均大于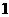 ”的( )
”的( )
A.充分但不必要条件 B.必要但不充分条件
C.充分必要条件 D.既不充分也不必要条件
答案:B
★ 抢 分 频 道 ★
基础巩固训练
10. (广东省黄岐高级中学2009届高三上学期月月考)
设集合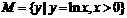 ,
,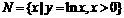 ,那么“
,那么“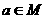 ”是“
”是“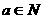 ”的( )
”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
答案:B
9.“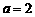 ” 是“函数
” 是“函数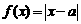 在区间
在区间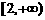 上为增函数”的 ( )
上为增函数”的 ( )
A.充分条件不必要 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
答案:A
题型2: 从集合思想或利用逆否命题判定
[例7] (广东省四会中学2009届高三上学期第一次质量检测)
“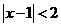 成立”是“
成立”是“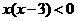 成立”的( )
成立”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
[解题思路]:当直接判断p是q什么条件较困难时, 可借助于集合或利用逆否命题来考虑 , 会更快捷和准确.
解析: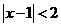 的解集是
的解集是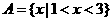 ,
,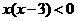 的解集是
的解集是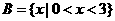
∵A B ∴选A
B ∴选A
[例8](广东省普宁市城东中学2009届高三上学期第三次月考)
若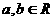 ,则
,则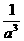
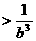 成立的一个充分不必要的条件是( )
成立的一个充分不必要的条件是( )
A.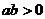 B.
B.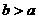 C.
C.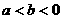 D.
D.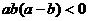
[解题思路]:
以选项为条件,要能得到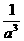
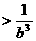 ,但反之不成立
,但反之不成立
解析:C 可以取反例,易得只有C答案
[名师指引]解答充分与必要条件问题时,要根据命题的特点,在三种方法(定义法、集合法和逆否命题法) 中选择一种进行判断,而且还依赖于问题本身所涉及到的具体数学内容的掌握与理解程度.
[新题导练]
8.(2009届省实高三次月考数学试题)
函数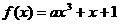 有极值的充要条件是 (
)
有极值的充要条件是 (
)
A.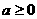 B.
B.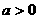 C.
C.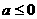 D.
D.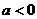
答案:D
7.若x、y、z均为实数,且a=x2-2y+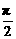 ,b=y2-2z+
,b=y2-2z+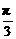 ,c=z2-2x+
,c=z2-2x+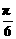 ,则a、b、c中是否至少有一个大于零?请说明理由.
,则a、b、c中是否至少有一个大于零?请说明理由.
分析:“a、b、c中是否至少有一个大于零”包括多种情况,正面解决很复杂,可考虑反面入手,利用反证法证明,但如何导出矛盾颇有技巧.
解:假设a、b、c都不大于0,即a≤0,b≤0,c≤0,则a+b+c≤0.
而a+b+c=x2-2y+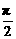 +y2-2z+
+y2-2z+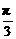 +z2-2x+
+z2-2x+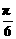 =(x-1)2+(y-1)2+(z-1)2+π-3,
=(x-1)2+(y-1)2+(z-1)2+π-3,
∵π-3>0,且无论x、y、z为何实数,
(x-1)2+(y-1)2+(z-1)2≥0,
∴a+b+c>0.这与a+b+c≤0矛盾.因此,a、b、c中至少有一个大于0.
考点二: 充要条件及其判定
题型1:利用定义作判断
[例6] (2008学年中山市一中高三年级统测试题)
在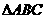 中,“
中,“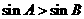 ”是“
”是“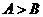 ”的
”的
A.充分而不必要条件 B. 必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
[解题思路]:判定p是q的充要条件,既要看“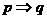 ”是否为真,又要看“
”是否为真,又要看“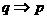 ”否为真, 只有都为真时, p才是q的充要条件.
”否为真, 只有都为真时, p才是q的充要条件.
解析:A “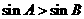 ”
” 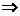 “
“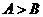 ”但反之不成立,故选A
”但反之不成立,故选A
[名师指引]定义判断的重要依据。
[新题导练]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com