
题目列表(包括答案和解析)
5.在△ABC中,a、b、c分别是角A、B、C的对边, 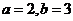 ,
, 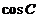 =
=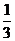 ,则其外接圆的半径为_______________.
,则其外接圆的半径为_______________.
[解析]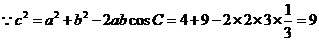 ,
,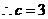
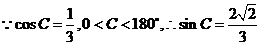
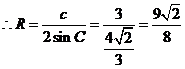
4. 若 中,
中,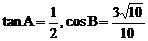 ,则角C的大小是__________
,则角C的大小是__________
解析
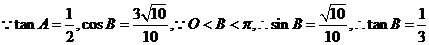
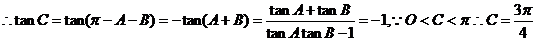
3.在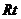 △ABC中,C=
△ABC中,C=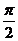 ,则
,则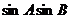 的最大值是_______________.
的最大值是_______________.
[解析] ∵在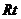 △ABC中,C=
△ABC中,C=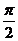 ,∴
,∴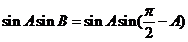
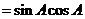
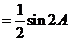 ,∵
,∵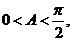 ∴
∴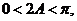 ∴
∴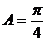 时,
时,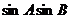 取得最大值
取得最大值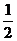 。
。
2. 在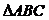 中,
中,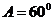 ,且最大边长和最小边长是方程
,且最大边长和最小边长是方程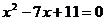 的两个根,则第三边的长为( )
的两个根,则第三边的长为( )
A.2 B.3 C.4 D.5
解析: [∵
[∵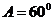 ,且最大边长和最小边长是方程
,且最大边长和最小边长是方程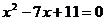 的两个根,则第三边为
的两个根,则第三边为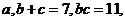 ∴
∴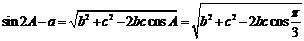
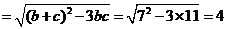 ]
]
1. 在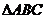 中,若
中,若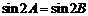 ,则
,则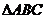 一定是( )
一定是( )
A、等腰三角形 B、直角三角形 C、等腰直角三角形 D、等腰或直角三角形
解析: [ ∵
[ ∵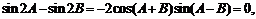 ∴
∴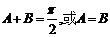 ]
]
8. 在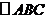 中,
中,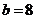 ,
,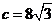 ,
,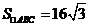 ,则
,则 等于
等于
A、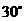 B、
B、 C、
C、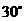 或
或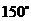 D、
D、 或
或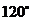
[解析]C
★ 抢 分 频 道 ★
基础巩固训练
7.在三角形 中,
中,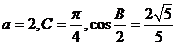 ,求三角形
,求三角形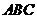 的面积
的面积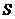 。
。
[解析] 由题意,得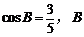 为锐角,
为锐角,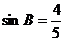 ,
,
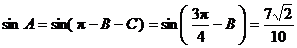 ,
,
由正弦定理得 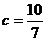 ,
, 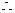
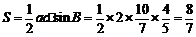 .
.
6.在Rt△ABC中,∠C=90°,且∠A,∠B,∠C所对的边a,b,c满足a+b=cx,求实数x的取值范围.
解析.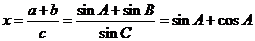
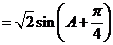 ,又
,又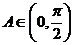
∴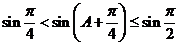 ,即
,即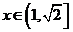
考点3 与三角形的面积相关的题
题型1:已知条件求面积
例1: (广州执信中学09届高三上学期期中考试)在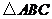 中,
中,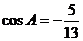 ,
,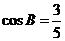 .
.
(Ⅰ)求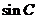 的值;(Ⅱ)设
的值;(Ⅱ)设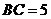 ,求
,求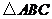 的面积.
的面积.
[解题思路]求角C的三角函数值可考虑用内角和定理;求三角形的面积直接用面积公式.
解析:(Ⅰ)由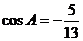 ,得
,得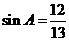 ,
,
由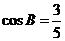 ,得
,得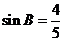 . 又
. 又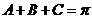
所以 .
.
(Ⅱ)由正弦定理得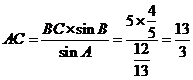 .
.
所以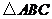 的面积
的面积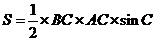
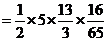
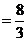 .
.
[名师指引]本题主要考查三角变换、余弦定理、三角形面积、解三角形等基础知识,考查运算求解能力.
题型2:已知面积求线段长或角
例2 (广东省惠州市2009届第二调研考试)在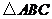 中,
中,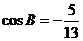 ,
,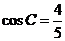 .
.
⑴、求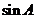 的值;
的值;
⑵、设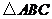 的面积
的面积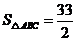 ,求
,求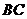 的长.
的长.
[解题思路]已知面积求边长或高,可考虑等积法.
解析:⑴、由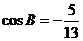 ,得
,得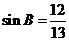 ,由
,由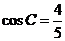 ,得
,得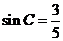 .
.
所以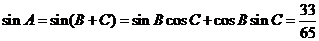 .
.
⑵、由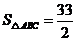 得
得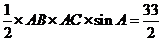 ,由⑴知
,由⑴知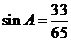 ,
,
故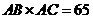 ,又
,又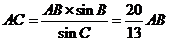 ,故
,故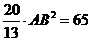 ,
,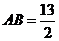 .
.
所以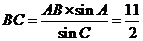 .
.
[名师指引]在处理解三角形的相关问题时,逆向思维也是必不可少的.
[新题导练]
5.三角形的三内角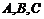 所对边的长分别为
所对边的长分别为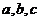 ,设向量
,设向量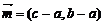 ,
,
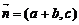 , 若
, 若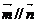 ,求角B的大小;
,求角B的大小;
解析:∵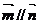 , ∴
, ∴ 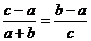 ∴
∴ 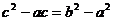
∴ 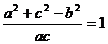
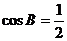 ,
, 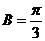
4. 在△ABC中,若=,则△ABC的形状是.( )
A.等腰直角三角形 B.直角三角形 C.等腰或直角三角形 D.等边三角形
解析:由已知=及正弦定理得=
∴sin2A=sin2B
∴2A=2B或2A+2B=π,即A=B或A+B=,
故△ABC为等腰三角形或直角三角形.选C
考点2: 三角形中的三角变换
题型:利用正、余弦定理和三角函数的恒等变换,进行边角互换,结合三角函数的图象与性质进行化简求值.
例1(08重庆)
设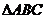 的内角A,B,C的对边分别为a,b,c,且A=
的内角A,B,C的对边分别为a,b,c,且A= ,c=3b.求:
,c=3b.求:
(Ⅰ)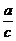 的值;(Ⅱ)cotB +cot C的值.
的值;(Ⅱ)cotB +cot C的值.
[解题思路]求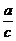 的值需要消去角和
的值需要消去角和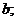 三角求值问题一般先考虑寻找角之间的关系
三角求值问题一般先考虑寻找角之间的关系
解析:(Ⅰ)由余弦定理得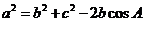 =
=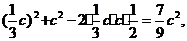
故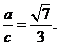
(Ⅱ)解法一: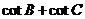 =
=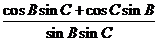 =
=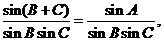
由正弦定理和(Ⅰ)的结论得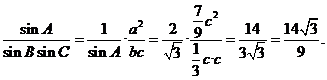
故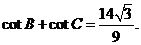
解法二:由余弦定理及(Ⅰ)的结论有
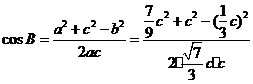 =
=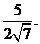
故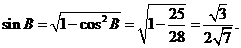
同理可得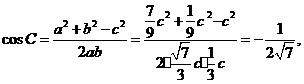
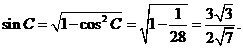
从而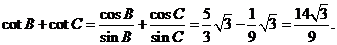
[名师指引]在解三角形的背景下一般见“切割就化弦”
[新题导练]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com