4.分布列:设离散型随机变量ξ可能取得值为

　　　　　　　　　　 x₁，x₂，…，x₃，…，

ξ取每一个值x_i(i=1，2，…)的概率为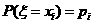，则称表

为随机变量ξ的_____________，简称ξ的分布列

答案:概率分布

3.连续型随机变量: 对于随机变量可能取的值，可以取某一区间内的一切值，这样的变量就叫做_____________.

答案:连续型随机变量

2. 离散型随机变量:对于随机变量可能取的值，可以按一定次序一一列出，这样的随机变量叫做_____________.

答案:离散型随机变量

1．随机变量：如果随机试验的结果可以用一个变量来表示，那么这样的变量叫做________.常用希腊字母ξ、η等表示

答案: 随机变量

12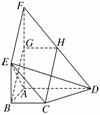．如图，平面ABEF⊥平面ABCD，四边形ABEF与ABCD都是直角梯形，∠BAD＝∠FAB＝90°，BC綊AD，BE綊FA，G、H分别为FA、FD的中点．

(1)证明：四边形BCHG是平行四边形；

(2)C、D、F、E四点是否共面？为什么？

解：(1)证明：由题设知，FG＝GA，FH＝HD，

所以GH綊AD.

又BC綊AD，

故GH綊BC，

所以四边形BCHG是平行四边形．

(2)C、D、F、E四点共面．理由如下：

由BE綊AF，G是FA的中点知，BE綊GF，

所以四边形EFGB是平行四边形，

所以EF∥BG.

由(1)知BG∥CH，所以EF∥CH，

故EC、FH共面．

又点D在直线FH上，

所以C、D、F、E四点共面．

11．如图所示，在正方体ABCD－A₁B₁C₁D₁中，E，F分别为A₁A，C₁C的中点，求证：四边形EBFD₁是菱形．

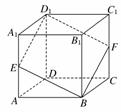
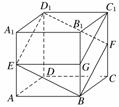证明：如图所示，取B₁B的中点G，

连结GC₁，EG，

∵GB綊C₁F，

∴四边形C₁FBG是平行四边形，

∴FB綊C₁G.

∵D₁C₁綊EG，

∴四边形D₁C₁GE为平行四边形．

∴GC₁綊D₁E，∴FB綊D₁E，

∴EBFD₁为平行四边形．

又∵FB＝FD₁，

∴四边形EBFD₁为菱形．

10．如图，已知平面α，β，且α∩β＝l.设梯形ABCD中，AD∥BC，且AB⊂α，CD⊂β.求证：AB，CD，l共点(相交于一点)．

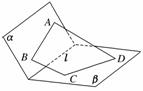
证明：∵梯形ABCD中，AD∥BC，

∴AB，CD是梯形ABCD的两腰

∴AB，CD必定相交于一点．

设AB∩CD＝M.

又∵AB⊂α，CD⊂β，∴M∈α，且M∈β，

∴M∈α∩β.

又∵α∩β＝l，∴M∈l，

即AB，CD，l共点．

9．(2010·淄博模拟)给出下面四个命题：

①“直线a∥直线b”的充要条件是“a平行于b所在的平面”；

②“直线l⊥平面α内所有直线”的充要条件是“l⊥平面α”；

③“直线a、b为异面直线”的充分而不必要条件是“直线a、b不相交”；

④“平面α∥平面β”的必要而不充分条件是“α内存在不共线三点到β的距离相等”．

其中真命题的序号是________．(写出所有真命题的序号)

解析：对于①，a可能在b所在的平面内，则由a∥b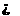a平行于b所在的平面，同样由a平行于b所在的平面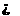a∥b，①错；易知②正确；对于③，直线a，b不相交，则a，b除了异面外还可能平行，③错；易知④正确．

答案：②④

8．(2011·浙江杭州)已知a、b为不垂直的异面直线，α是一个平面，则a、b在α上的射影可能是：①两条平行直线；②两条互相垂直的直线；③同一条直线；④一条直线及其外一点．则在上面的结论中，正确结论的编号是________(写出所有正确结论的编号)．

解析：①、②、④对应的情况如下：

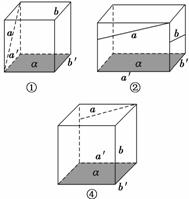
用反证法证明③不可能．

答案：①②④

7．平面α、β相交，在α、β内各取两点，这四点都不在交线上，这四点能确定________个平面．

解析：分类，如果这四点在同一平面内，那么确定一个平面，如果这四点不共面，则任意三点可确定一个平面，所以可确定四个．

答案：1或4