
题目列表(包括答案和解析)
4.已知: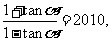 求证:
求证: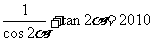
解: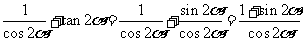
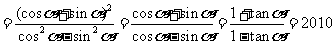 .
.
3.化简: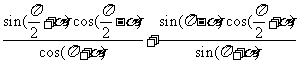 .
.
解析:0 [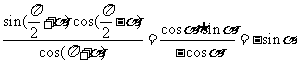 ,
,
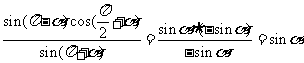 ,故原式=
,故原式=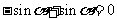 ]
]
2.(中山市高三级2008-2009学年度第一学期期末统一考试)若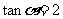 ,则
,则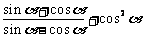 =
.
=
.
解析: 原式=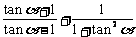 =
=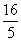
考点2 化简与证明问题
题型1:三角式的化简
[例3]化简: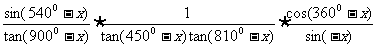
[解题思路]利用诱导公式及三角变换公式化简三角函数式
[解析] 原式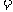
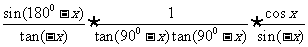
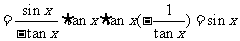
[名师指引]化简三角函数式.化简是一种不指明答案的恒等变形,三角函数化为最简形式的标准是相对的,一般是指函数种类要最少,项数要最少,函数次数尽量低,能求出数值的要求出数值,尽量使分母不含三角形式和根式.
题型2:三角恒等式的证明
例4.求证: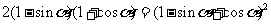
[解题思路]将右边展开进行因式分解.
证明:右边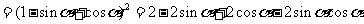
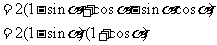
[名师指引]证明简单的三角恒等式.一般方法有三种:即由繁的一边证到简单的一边;证明左、右两边等于同一式子;证明与原恒等式等价的式子,从而推出原式成立.在化简或证明三角函数式时常用的技巧有:
(1)“1”的代换.为了解题的需要有时可以将1用“ ”代替.
”代替.
(2)切化弦.利用商数关系把正切化为正弦和余弦函数.
(3)整体代替.将计算式适当变形使条件可以整体代入或将条件适当变形找出与算式之间的关系.
题型3:条件三角等式的证明
例5.已知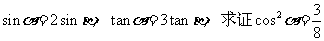
[解题思路]已知条件中含角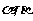 ,待求结论只含
,待求结论只含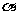 ,故考虑消元法
,故考虑消元法
证:由题设: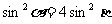 ①
①
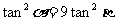 ②
②
①/②: 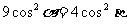 ③
③
①+③: 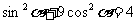

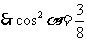
[名师指引] 等式中出现正弦、余弦和正切函数,一般采用“切化弦”的方法进行证明.若已知条件中的角多于待求结论中的角可考虑消元法.
[新题导练]
1.
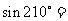 ( )
( )
A.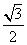 B.
B.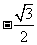 C.
C.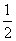 D.
D.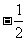
解析.sin2100 =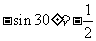 ,选D。
,选D。
3.重难点:通过审题分析已知条件和待求结论之间角的关系,确定好符号,使问题获解。
(1). 对三角函数诱导公式不完全理解,不加讨论而导致错误.
问题1:化简: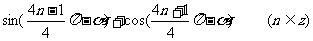
错解:原式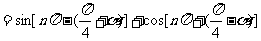

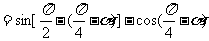
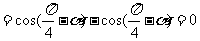
正解:原式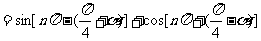
(1)当 ,时
,时
原式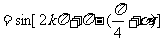 +
+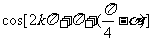
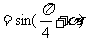
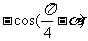
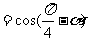
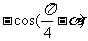 =0
=0
(2)当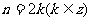 ,时
,时
原式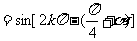 +
+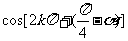
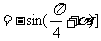 +
+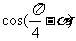 =0
=0
(2)要注意角的范围,防止符号取错.
问题2:已知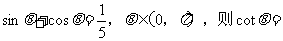 __________
__________
错解:两边同时平方,由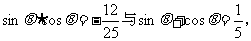 得
得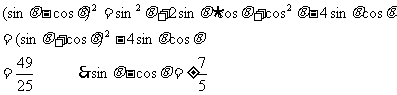
∴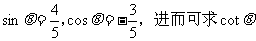 解得:
解得: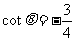
或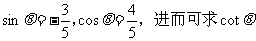 解得:
解得: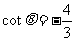
所以 的值为正而导致错误.
的值为正而导致错误.
正解: 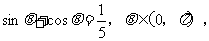
两边同时平方,有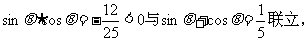
求出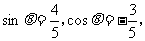 ∴
∴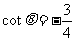
★热 点 考 点 题 型 探 析
考点1 求值问题
题型:利用公式求三角式的值
[例1](广东省执信中学2009届高三上学期期中考试)tan600°的值是( )
A.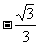 B.
B.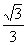 C.
C.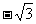 D.
D.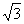
[解题思路]由于6900超出了锐角的范围,故需先利用诱导公式进行化简.
[解析]由tan6900=tan(-300+2×3600)=tan(-300)=-tan300=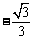 知应选A.
知应选A.
[名师指引]应用诱导公式,重点是“函数名称”与“正负号”的正确判断.
[例2].(2007·韶关市高三摸底题)已知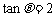 ,则
,则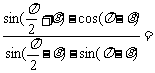 ( )
( )
A、2 B、-2 C、0 D、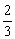
[解题思路]联想到诱导公式及对同角三角函数公式解题
解析:B[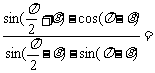
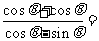
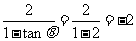
[名师指引]处理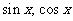 的齐次式的问题,通常采用化切法,即将分子分母或等式两边同除以
的齐次式的问题,通常采用化切法,即将分子分母或等式两边同除以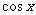 的最高次幂化为
的最高次幂化为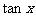 的关系式即可,这种题型高考中经常考。
的关系式即可,这种题型高考中经常考。
[新题导练]
2.难点:正确的使用同角三角函数的关系式和诱导公式。
1.重点:掌握利用同角三角函数的关系式和诱导公式三角式化简,求值与证明等问题。
3. 关于诱导公式
(1)诱导公式(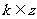 )
)
|
角
函数 |
正弦 |
余弦 |
记忆口诀 |
 |
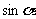 |
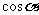 |
函数名不变 符号看象限 |
 |
-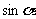 |
-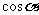 |
|
 |
-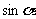 |
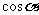 |
|
 |
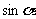 |
-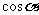 |
|
 |
-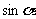 |
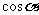 |
|
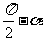 |
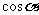 |
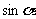 |
函数名不变 符号看象限 |
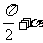 |
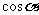 |
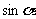 |
|
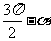 |
-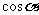 |
-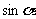 |
|
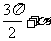 |
-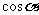 |
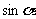 |
(2)求任意角的三角函数值的问题,都可以通过诱导公式化为锐角三角函数的求值问题,具体步骤为“负角化正角”→“正角化锐角”→求值.

(3)诱导公式解决常见题型
(A)求值:已知一个角的某个三角函数,求这个角其他三角函数;
(B)化简:要求是能求值则求值,次数、种类尽量少,尽量化去根式,尽可能不含分母.
★重 难 点 突 破
2.用同角三角函数的基本关系式求值时应注意:
①注意“同角”,至于角的形式无关重要,如 等;
等;
②注意这些关系式都是对于使它们有意义的角而言的,如
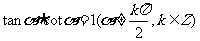 ;
;
③对这些关系式不仅要牢固掌握,还要能灵活运用(正用、反用、变形用),如:
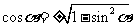 ,
, 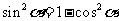 ,
, 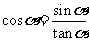 等。
等。
1.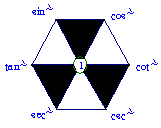 同角三角函数的基本关系式的记忆法则
同角三角函数的基本关系式的记忆法则
(1)对角线上对应的函数互为倒数;
(2)每一个顶点对应函数等于相邻顶点对应函数的乘积;
(3)阴影三角形中,上面二个顶点对应的函数的平方和等
于下面一个顶点的平方。
例如: 1
1
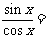
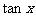
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com