
题目列表(包括答案和解析)
3. 第一次击中,第二次未击中,第三次击中,
点评:本题主要考查相互独立事件同时发生或互斥事件发生的概率的计算方法,考查运用概率知识解决实际问题的能力.
备选取
2. 第一次未击中目标,第二、三次击中,
1. 前三次都击中目标,第四、五次连续两次都未击中目标
21. (本题满分12分)甲、乙两人各射击一次,击中目标的概率分别是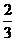 和
和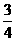 。假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响。
。假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响。
(Ⅰ)求甲射击4次,至少1次未击中目标的概率;
(Ⅱ)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;
(Ⅲ)假设两人连续两次未击中目标,则停止射击。问:乙恰好射击5次后,被中止射击的概率是多少?
思路分析:本题是一道概率综合运用问题,第一问中求“至少有一次末击中问题”可从反面求其概率问题;第二问中先求出甲恰有两次末击中目标的概率,乙恰有3次末击中目标的概率,再利用独立事件发生的概率公式求解.第三问设出相关事件,利用独立事件发生的概率公式求解,并注意利用对立、互斥事件发生的概率公式.
解: (Ⅰ)记“甲连续射击4次,至少1次未击中目标”为事件A1,
由题意,射击4次,相当于4次独立重复试验,
故P(A1)=1- P( )=1-
)=1-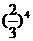 =
=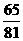 。
。
答:甲射击4次,至少1次未击中目标的概率为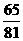 ;……4分
;……4分
(Ⅱ) 记“甲射击4次,恰好击中目标2次”为事件A2,
“乙射击4次,恰好击中目标3次”为事件B2,则
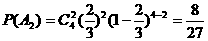 ,
,
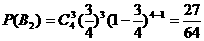 ,
,
由于甲、乙射击相互独立,
故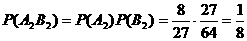 。
。
答:两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率为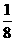 ;…………8分
;…………8分
(Ⅲ)记“乙恰好射击5次后,被中止射击”为事件A3,
“乙第i次射击未击中” 为事件Di,(i=1,2,3,4,5),则A3=D5D4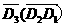 ,且P(Di)=
,且P(Di)=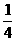 ,
,
由于各事件相互独立,
故P(A3)= P(D5)P(D4)P(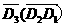 )
)
=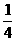 ×
×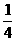 ×
×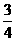 ×(1-
×(1-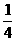 ×
×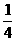 )
)
=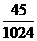 ,
,
答:乙恰好射击5次后,被中止射击的概率是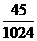 。…………12分
。…………12分
或者:分类处理
20. (本题满分14分)一个口袋中装有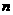 个红球(
个红球(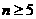 且
且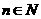 )和5个白球,一次摸奖从中摸两个球,两个球颜色不同则为中奖.
)和5个白球,一次摸奖从中摸两个球,两个球颜色不同则为中奖.
(Ⅰ)试用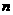 表示一次摸奖中奖的概率
表示一次摸奖中奖的概率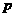 ;
;
(Ⅱ)若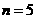 ,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率;
,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率;
(Ⅲ)记三次摸奖(每次摸奖后放回)恰有一次中奖的概率为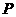 .当
.当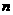 取多少时,
取多少时,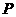 最大?
最大?
(Ⅰ)一次摸奖从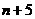 个球中任选两个,有
个球中任选两个,有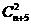 种,
种,
它们等可能,其中两球不同色有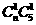 种,………………………2分
种,………………………2分
一次摸奖中奖的概率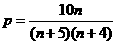 .………………………4分
.………………………4分
(Ⅱ)若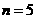 ,一次摸奖中奖的概率
,一次摸奖中奖的概率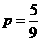 ,………………………6分
,………………………6分
三次摸奖是独立重复试验,三次摸奖(每次摸奖后放回)恰有一次中奖的概率是
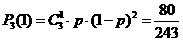 . ………………………8分
. ………………………8分
(Ⅲ)设每次摸奖中奖的概率为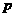 ,则三次摸奖(每次摸奖后放回)恰有一次中奖的概率为
,则三次摸奖(每次摸奖后放回)恰有一次中奖的概率为
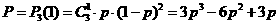 ,
,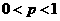 , ……………………12分
, ……………………12分
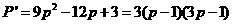 ,知在
,知在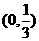 上
上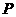 为增函数,在
为增函数,在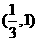 上
上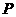 为减函数,当
为减函数,当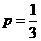 时
时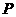 取得最大值.又
取得最大值.又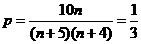 ,解得
,解得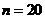 .…………14分
.…………14分
答:当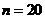 时,三次摸奖(每次摸奖后放回)恰有一次中奖的概率最大.
时,三次摸奖(每次摸奖后放回)恰有一次中奖的概率最大.
[方法探究]本题是一个在等可能性事件基础上的独立重复试验问题,体现了不同概型的综合.第Ⅲ小题中的函数是三次函数,运用了导数求三次函数的最值.如果学生直接用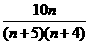 代替
代替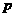 ,函数将比较烦琐,这时需要运用换元的方法,将
,函数将比较烦琐,这时需要运用换元的方法,将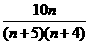 看成一个整体,再求最值.
看成一个整体,再求最值.
19. (本题满分14分)某社区举办北京奥运知识宣传活动,现场的“抽卡有奖游戏”特别引人注目,游戏规则是:盒子中装有8张形状大小相同的精美卡片,卡片上分别印有“奥运福娃”或“奥运会徽”,要求4人中一组参加游戏,参加游戏的4人从盒子中轮流抽取卡片,一次抽2张,抽取后不放回,直到4人中一人一次抽到2张“奥运福娃” 卡才能得到奖并终止游戏。
(1)游戏开始之前,一位高中生问:盒子中有几张“奥运会徽” 卡?主持人说:若从盒中任抽2张卡片不都是“奥运会徽”
卡的概率为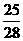 ,请你回答有几张“奥运会徽” 卡呢?
,请你回答有几张“奥运会徽” 卡呢?
(2)现有甲、乙、丙、丁4人参加游戏,约定甲、乙、丙、丁依次抽取。用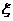 表示4人中的某人获奖终止游戏时总共抽取卡片的次数,求
表示4人中的某人获奖终止游戏时总共抽取卡片的次数,求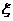 的概率分布及
的概率分布及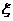 的数学期望。
的数学期望。
解:(1)设盒子中有“会徽卡”n张,依题意有,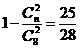
解得n=3
即盒中有“会徽卡”3张。……4分
(2)因为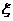 表示某人一次抽得2张“福娃卡”终止时,所有人共抽取了卡片的次数,所以
表示某人一次抽得2张“福娃卡”终止时,所有人共抽取了卡片的次数,所以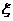 的所有可能取值为1,2,3,4,……4分
的所有可能取值为1,2,3,4,……4分
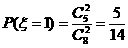 ;
;
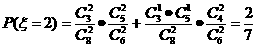 ;
;
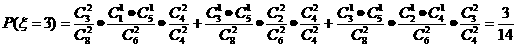 ;
;
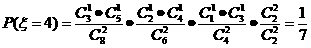 ,
,
概率分布表为:
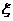 |
1 |
2 |
3 |
4 |
|
P |
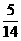 |
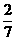 |
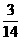 |
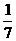 |
……10分
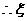 的数学期望为
的数学期望为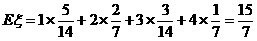 。……14分
。……14分
18. (本题满分13分) 在2008年春运期间,一名大学生要从广州回到郑州老家有两种选择,即坐火车或汽车。已知该大学生先去买火车票的概率是先去买汽车票概率的3倍,汽车票随时都能买到。若先去买火车票,则买到火车票的概率为0.6,买不到火车票,再去买汽车票。
(I)求这名大学生先去买火车票的概率;
(II)若火车票的价格为120元,汽车票的价格为280元,设该大学生购买车票所花费钱数为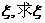 的期望值。
的期望值。
解:(I)设先去买火车票的概率为P(A),先去买汽车票的概率为P(B),
则由条件可知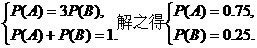
即先去买火车票的概率为0.75. …………4分
(II)解:该大学生首先到火车站且买到火车票的概率为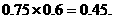
…………6分
∴该大学生买汽车票的概率为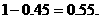 …………8分
…………8分
设该大学生购买车票所花费钱数为ξ,可得ξ的分布列如下:
|
ξ |
120 |
280 |
|
P |
0.45 |
0.55 |
∴该大学生购买车票所花费钱数的期望值为
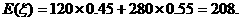 …………13分
…………13分
17. (本题满分13分)(新华网)反兴奋剂的大敌、服药者的宠儿--HGH(人体生长激素),有望在2008年8月的北京奥运会上首次“伏法”。据悉,国际体育界研究近10年仍不见显著成效的HGH检测,日前已取得新的进展,新生产的检测设备有希望在北京奥运会上使用.若组委会计划对参加某项比赛的12名运动员的血样进行突击检查,采用如下化验方法:将所有待检运动员分成若干小组,每组m个人,再把每个人的血样分成两份,化验时将每个小组内的m个人的血样各一份混合在一起进行化验,若结果中不含HGH成分,那么该组的m个人只需化验这一次就算检验合格;如果结果中含有HGH成分,那么需要对该组进行再次检验,即需要把这m个人的另一份血样逐个进行化验,才能最终确定是否检验合格,这时,对这m个人一共需要进行m+1次化验.假定对所有人来说,化验结果中含有HGH成分的概率均为 .当m=3时,求: (1)一个小组只需经过一次检验就合格的概率; (2)至少有两个小组只需经过一次检验就合格的概率(精确到0.01.参考数据:0.2713≈0.020,0.2714≈0.005,0.7292≈0.500)
解:(1)一个小组经过一次检验就合格,则必有此三人的血样中都不含HGH成分
∴所求概率为P=(1-)3=0.729 ………6分
(2)依据题意,至少有两个小组只需经过一次检验就合格的概率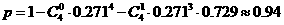 ………13分
………13分
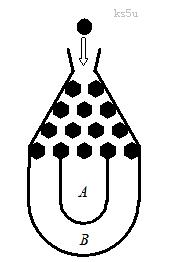
16. (本题满分13分) 将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落的过程中,将3次遇到黑色障碍物,最后落入 袋或
袋或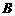 袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是
袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是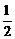 .
.
(Ⅰ)求小球落入 袋中的概率
袋中的概率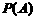 ;
;
(Ⅱ)在容器入口处依次放入4个小球,记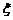 为落入
为落入 袋中的小球个数,试求
袋中的小球个数,试求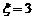 的概率和
的概率和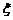 的数学期望
的数学期望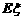 .
.
解:(Ⅰ)记“小球落入 袋中”为事件
袋中”为事件 ,“小球落入
,“小球落入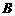 袋中”为事件
袋中”为事件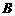 ,则事件
,则事件 的对立事件为
的对立事件为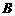 ,而小球落入
,而小球落入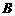 袋中当且仅当小球一直向左落下或一直向右落下,故
袋中当且仅当小球一直向左落下或一直向右落下,故
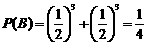 ,
,
从而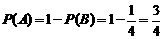 ;…………6分
;…………6分
(Ⅱ)显然,随机变量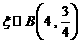 ,故
,故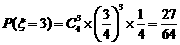 ,…………13分
,…………13分
15.(选做题) 有一批产品,其中有12件正品和4件次品,从中任取3件,若ξ表示取到次品的个数,则Dξ=
答案: 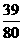
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com