
题目列表(包括答案和解析)
10. 数列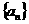 满足
满足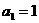 且
且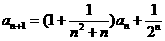
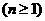 .
.
用数学归纳法证明: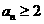
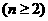 ;
;
[证明](1)①当n=2时,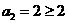 ,不等式成立.
,不等式成立.
②假设当n=k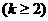 时不等式成立,即
时不等式成立,即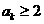 (
(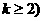 ,
,
那么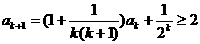 .
.
这就是说,当n=k+1时不等式成立.根据①②可知: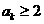 对所有
对所有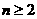 成立.
成立.
9. 在数列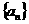 中,
中,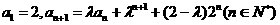 ,其中
,其中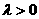 ,求数列
,求数列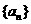 的通项公式
的通项公式
[解析] 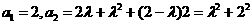 ,
,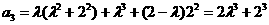 ,
,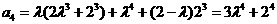 .由此可猜想出数列
.由此可猜想出数列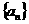 的通项公式为
的通项公式为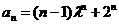 .
.
以下用数学归纳法证明:(1)当n=1时,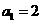 ,等式成立.
,等式成立.
(2)假设当n=k时等式成立,即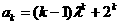 .则当n=k+1时,
.则当n=k+1时,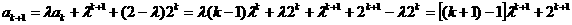 .这就是说,当n=k+1时等式也成立。由(1)(2)可知数列
.这就是说,当n=k+1时等式也成立。由(1)(2)可知数列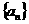 的通项公式
的通项公式
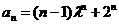
8. 证明: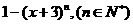 能被
能被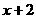 整除
整除
[解析] (1)当n=1时,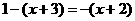 ,能被
,能被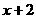 整除;
整除;
(2)假设n=k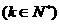 时命题成立,即
时命题成立,即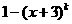 能被
能被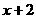 整除
整除
则可设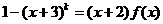 (其中
(其中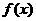 为
为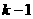 次多项式)
次多项式)
当当n=k+1时,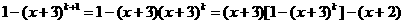
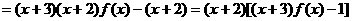 能被
能被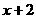 整除
整除
所以,当n=k+1时,命题仍然成立
由(1)(2)可知,对于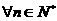 命题依然成立.
命题依然成立.
7. 求证: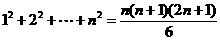
[证明](1)当n=1时,左端=1 ,右端=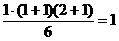 ,左端=右端,等式成立;
,左端=右端,等式成立;
(2)假设n=k时,等式成立,即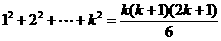 ,则
,则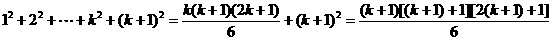 .所以,当n=k+1时,等式仍然成立
.所以,当n=k+1时,等式仍然成立
由(1)(2)可知,对于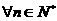 等式依然成立.
等式依然成立.
6.若存在正整数 ,使得
,使得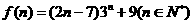 能被
能被 整除,则
整除,则 =
=
[解析]36. [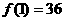
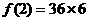
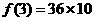 ,猜想:
,猜想: =36]
=36]
综合提高训练
5.设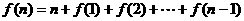 ,用数学归纳法证明“
,用数学归纳法证明“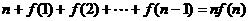 ”时,第一步要证的等式是
”时,第一步要证的等式是
[解析] 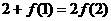
4. 如果命题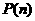 对n=k成立,则它对n=k+1也成立,现已知
对n=k成立,则它对n=k+1也成立,现已知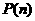 对n=4不成立,则下列结论中正确的是(
)
对n=4不成立,则下列结论中正确的是(
)
A. 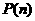 对
对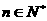 成立 B.
成立 B. 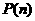 对n>4且
对n>4且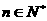 成立
成立
C. 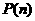 对n<4且
对n<4且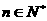 成立 D.
成立 D. 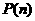 对n
对n 4且
4且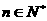 不成立
不成立
[解析] D
3. 凸n边形有f(n)条对角线,则凸n+1边形有对角线数f(n+1)为( )
A.f(n)+n+1 B.f(n)+n C.f(n)+n-1 D.f(n)+n-2
[解析] C
2.用数学归纳法证明:1+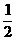 +
+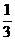 +
+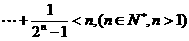 时,在第二步证明从n=k到n=k+1成立时,左边增加的项数是( )
时,在第二步证明从n=k到n=k+1成立时,左边增加的项数是( )
A.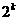 B.
B.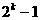
 C.
C.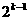 D.
D.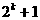
[解析] 项数为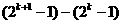 ,选A
,选A
1.用数学归纳法证明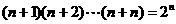
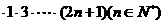 ,从“k到k+1”左端需乘的代数式是( )
,从“k到k+1”左端需乘的代数式是( )
A.2k+1
B.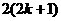 C.
C.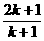 D.
D.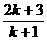
[解析] 左端需乘的代数式是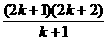 =
=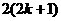 ,选B
,选B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com