3.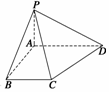如图所示，四棱锥P-ABCD中，PA⊥平面ABCD，PB与底面所成的角为45°，

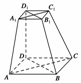
底面ABCD为直角梯形，∠ABC=∠BAD=90°,PA=BC=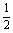AD.

(1)求证：平面PAC⊥平面PCD；

(2)在棱PD上是否存在一点E，使CE∥平面PAB？若存在，请确定E点的位置；若不存在，请说明理由.

回顾总结

知识

方法

思想

2.如图，在六面体ABCD-A₁B₁C₁D₁中，四边形ABCD是边长为2的正方形，四边

形A₁B₁C₁D₁是边长为1的正方形，DD₁⊥平面A₁B₁C₁D₁，DD₁⊥平面ABCD，DD₁=2.

求证：(1)A₁C₁与AC共面，B₁D₁与BD共面；

(2)平面A₁ACC₁⊥平面B₁BDD₁.

1.如图所示，平面PAD⊥平面ABCD，ABCD为正方形，△PAD是直角三角形，且PA=AD=2，

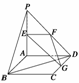E、F、G分别是线段PA、PD、CD的中点.

求证：PB∥平面EFG.

5.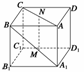如图所示,在正方体ABCD-A₁B₁C₁D₁中,棱长为a,M,N分别为A₁B和AC上的点,A₁M=AN=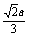,则MN与平面BB₁C₁C的位置关系是　　　　　 .

例题精讲

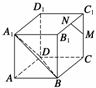例1如图所示，在正方体ABCD-A₁B₁C₁D₁中，M、N分别是C₁C、B₁C₁的中点.

求证：MN∥平面A₁BD.

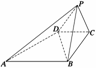例2　 如图所示,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,

AB=BC=PB=PC=2CD,侧面PBC⊥底面ABCD.证明:

(1)PA⊥BD;

(2)平面PAD⊥平面PAB.

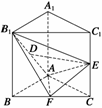例3　 如图所示，已知直三棱柱ABC-A₁B₁C₁中，△ABC为等腰直角三角形，

∠BAC=90°，且AB=AA₁，D、E、F分别为B₁A、C₁C、BC的中点.

求证：

(1)DE∥平面ABC；(2)B₁F⊥平面AEF.

巩固练习

4.已知a=(1,1,1),b=(0,2,-1),c=ma+nb+(4,-4,1).若c与a及b都垂直，则m,n的值分别为　　 　　.

3.向量a=(-2,-3,1),b=(2,0,4),c=(-4，-6，2)，下列结论不正确的是　　　 .

①a∥b，b⊥c　 ，②a∥b，a⊥c，③a∥c，a⊥b，④以上都不对

2.已知直线l的方向向量为v，平面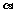的法向量为u,则v·u=0，l与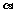的关系是　　　　 .

1.设平面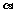的法向量为(1，2，-2)，平面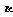的法向量为(-2，-4，k)，若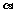∥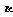，则k=　　　　 　　.

20.(16分)设p：实数x满足x²-4ax+3a²<0,其中a<0；q：实数x满足x²-x-6≤0，或x²+2x-8＞0，且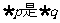的必

不充分条件，求a的取值范围.　

19.(16分)记函数f(x)=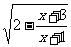的定义域为A，g(x)=lg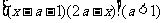的定义域为B.

(1)求A；

(2)若B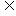A，求实数a的取值范围.