2．(2011·深圳调研)若曲线C：x²+y²+2ax－4ay+5a²－4＝0上所有的点均在第二象限内，则a的取值范围为(　)

A．(－∞，－2)　 　　　　　　　 B．(－∞，－1)

C．(1，+∞)　 　　　　　　 D．(2，+∞)

解析：曲线C的方程可化为：(x+a)²+(y－2a)²＝4，其圆心为(－a,2a)，要使得圆C的所有的点均在第二象限内，则圆心(－a,2a)必须在第二象限，从而有a>0，并且圆心到两坐标轴的最短距离应该大于圆C的半径，易知圆心到横、纵坐标轴的最短距离为|2a|，|－a|，则有|2a|>2，|－a|>2，故a>2.

答案：D

1．方程x²+y²+ax+2ay+2a²+a－1＝0表示圆，则a的取值范围是(　)

A．a<－2或a>　　　 B．－<a<0

C．－2<a<0　 　　　　　　　　　　 D．－2<a<

解析：由a²+4a²－4(2a²+a－1)>0知－3a²－4a+4>0即3a²+4a－4<0

∴－2<a<.

答案：D

12．已知m∈R，直线l：mx－(m²+1)y＝4m和圆C：x²+y²－8x+4y+16＝0.

(1)求直线l斜率的取值范围；

(2)直线l能否将圆C分割成弧长的比值为的两段圆弧？为什么？

解：(1)直线l的方程可化为y＝x－，直线l的斜率k＝，

因为|m|≤(m²+1)，

所以|k|＝≤，当且仅当|m|＝1时等号成立．

所以斜率k的取值范围是[－，]．

(2)不能．

由(1)知l的方程为y＝k(x－4)，其中|k|≤.

圆C的圆心为C(4，－2)，半径r＝2.

圆心C到直线l的距离d＝.

由|k|≤，得d≥＞1，即d＞.

从而，若l与圆C相交，则圆C截直线l所得的弦所对的圆心角小于.

所以l不能将圆C分割成弧长的比值为的两段弧．

11．已知圆x²+y²－4x+2y－3＝0和圆外一点M(4，－8)．

(1)过M作圆的割线交圆于A、B两点，若|AB|＝4，求直线AB的方程；

(2)过M作圆的切线，切点为C、D，求切线长及CD所在直线的方程．

解：(1)圆即(x－2)²+(y+1)²＝8，

圆心为P(2，－1)，半径r＝2.

①若割线斜率存在，设AB：y+8＝k(x－4)，即kx－y－4k

－8＝0，设AB的中点为N，则|PN|＝＝，

由|PN|²+²＝r²，得k＝－，

AB：45x+28y+44＝0.

②若割线斜率不存在，AB：x＝4，代入圆方程得y²+2y－3＝0，y₁＝1，y₂＝－3符合题意，综上，直线AB的方程为45x+28y+44＝0或x＝4.

(2)切线长为＝＝3.

以PM为直径的圆的方程为

(x－2)(x－4)+(y+1)(y+8)＝0，

即x²+y²－6x+9y+16＝0.

又已知圆的方程为x²+y²－4x+2y－3＝0，

两式相减，得2x－7y－19＝0，

所以直线CD的方程为2x－7y－19＝0.

10．已知点M(3,1)，直线ax－y+4＝0及圆(x－1)²+(y－2)²＝4.

(1)求过M点的圆的切线方程；

(2)若直线ax－y+4＝0与圆相切，求a的值；

(3)若直线ax－y+4＝0与圆相交于A，B两点，且弦AB的长为2，求a的值．

解：(1)由题意可知M在圆(x－1)²+(y－2)²＝4外，

故当x＝3时满足与圆相切．

当斜率存在时设为y－1＝k(x－3)，即kx－y－3k+1＝0.

由＝2，∴k＝，

∴所求的切线方程为x＝3或3x－4y－5＝0.

(2)由ax－y+4＝0与圆相切知＝2，

∴a＝0或a＝.

(3)圆心到直线的距离d＝，

又l＝2，r＝2，

∴由r²＝d²+()²，可得a＝－.

9．(2010·浙江教育考试院)设直线3x+4y－5＝0与圆C₁：x²+y²＝4交于A，B两点，若圆C₂的圆心在线段AB上，且圆C₂与圆C₁相切，切点在圆C₁的劣弧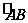上，则圆C₂的半径的最大值是________．

解析：由题意结合圆的性质得当圆C₂的圆心C₂为AB的中点时圆C₂的半径最大．而原点到直线3x+4y－5＝0的距离为1，圆C₂过原点O，所以圆C₂的半径最大值为1.

答案：1

8．已知圆C₁：x²+y²－6x－7＝0与圆C₂：x²+y²－6y－27＝0相交于A、B两点，则线段AB的中垂线方程为________．

解析：AB的中垂线即为圆C₁、圆C₂的连心线C₁C₂，又C₁(3,0)，C₂(0,3)，C₁C₂的方程为x+y－3＝0，即线段AB的中垂线方程为x+y－3＝0.

答案：x+y－3＝0

7．过点(0,1)的直线与x²+y²＝4相交于A、B两点，则|AB|的最小值为________．

解析：当过点(0,1)，(0,0)的直线与弦AB垂直时，|AB|的最小值为2.

答案：2

6．把直线x－y+1＝0沿向量a＝(1,0)方向平移，使之与圆(x－2)²+(y－1)²＝1相切，则平移的距离为(　)

A.－1　 　　　　　　　　　　　　 B.+2

C.－1与+1　 　　　　　　 D．2－与2+

解析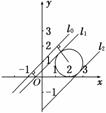：如图，将直线l₀：x－y+1＝0沿向量a＝(1,0)方向平移到l₁或l₂时，直线与圆相切，因为圆心(2,1)到直线l₀的距离d＝＝，圆的半径为1，所以直线l₀与l₁的距离为－1，直线l₀与l₂的距离为+1，故沿向量a＝(1,0)方向平移的距离为×(－1)＝2－与×(+1)＝2+.

答案：D

5．(2010·宝鸡五月质检)已知直线x+y＝a与圆x²+y²＝4交于A，B两点，且|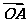+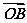|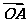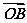＝|－|(其中O为坐标原点)，则实数a等于(　)

A．2 　　　　　　　　　　　　　 　B．－2

C．2或－2 　　　　　　　　 　D.或－

解析：由|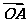+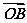|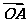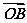＝|－|知OA⊥OB，所以由题意可得＝，所以a＝±2.

答案：C