1．(2009·湖南师大附中)a、b为实数，集合M＝{，1}，N＝{a,0}，f：x→2x表示把集合M中的元素x，映射到集合N中为2x，则a+b＝　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．－2　　B．0　　C．2　　D．±2

答案：C

解析：由于M中元素只能对应0,1只能对应a，所以＝0，a＝2，所以b＝0，a＝2，因此a+b＝2，故选C.

16．唐山市营业区内住宅电话通话费为前3分钟0.20元，以后每分钟0.10元，(不足3分钟按3分钟计，以后不足1分钟按1分钟计)．

(1)在所给坐标系中，画出一次通话在6分钟内(包括6分钟)的通话费y(元)关于通话时间t(分钟)的函数图象；

(2)如果一次通话t分钟(t>0)，写出通话费y(元)关于通话时间t(分钟)的函数关系式：(可用符号<t>表示不小于t的最小整数)；

(3)如果需要通话时间较长，可以采用分若干次拨打的方法，某人通话91分钟，计算这个人用最省钱的拨打方法比用一次拨打方法少花多少钱？

解析：(1)

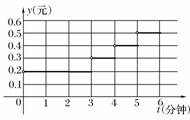
(2)y＝

其中<t－3>表示不超过t－3的最大整数．

(3)一次拨打费用Y＝0.2+＜91－3＞×0.1＝9(元)．

分30次拨打，29次每次通话都是3分钟，只有1次通话4分钟其费用y＝30×0.2+0.1＝6.1(元)．

这样少花钱Y－y＝2.9(元)．

15．已知函数f(x)＝－，

(1)求证：函数y＝f(x)的图象关于点(，－)对称；

(2)求f(－2)+f(－1)+f(0)+f(1)+f(2)+f(3)的值．

证明：设P(x，y)是y＝f(x)的图象上任意一点，它关于点(，－)的对称点的坐标为(1－x，－1－y)，

由已知y＝－，

则－1－y＝－1+＝－，

又f(1－x)＝－＝－，

∴－1－y＝f(1－x)，即函数y＝f(x)的图象关于点(，－)对称．

(2)由(1)有f(1－x)＝－1－f(x)即f(x)+f(1－x)＝－1.

∴f(－2)+f(3)＝－1，f(－1)+f(2)＝－1，f(0)+f(1)＝－1，

则f(－2)+f(－1)+f(0)+f(1)+f(2)+f(3)＝－3.

14．(1)已知f(+1)＝x+2，求f(x)，f(x+1)，f(x²)；

(2)已知2f(x)+f()＝10^x，求f(x)．

分析：(1)用换元法，设t＝+1≥1或配凑法．

(2)构造关于f(x)和f()的方程组，利用消元法消去f()解出f(x)．

解析：(1)方法一：换元法

设t＝+1≥1，则＝t－1(t≥1)，

x＝(t－1)²，

∴f(t)＝(t－1)²+2(t－1)＝t²－1(t≥1)，

∴f(x)＝x²－1(x≥1)，

∴f(x+1)＝(x+1)²－1＝x²+2x(x≥0)，

f(x²)＝x⁴－1(x≤－1或x≥1)．

方法二：配凑法

∵f(+1)＝x+2＝(+1)²－1，

∴f(x)＝x²－1(x≥1)，以下同方法一．

(2)由2f(x)+f()＝10^x，用代换x，

则2f()+f(x)＝10，

两式联立消去f()得f(x)＝×10^x－×10.

13．(1)求函数f(x)＝的定义域；

(2)已知函数f(2^x)的定义域是[－1,1]，求f(log₂x)的定义域．

解析：(1)要使函数有意义，则只需要：

，即，

解得－3＜x＜0或2＜x＜3.

故函数的定义域是(－3,0)∪(2,3)．

(2)∵y＝f(2^x)的定义域是[－1,1]，

即－1≤x≤1，∴≤2^x≤2.

∴函数y＝f(log₂x)中≤log₂x≤2.

即log₂≤log₂x≤log₂4，∴≤x≤4.

故函数f(log₂x)的定义域为[，4]．

12．已知函数f(x)＝的定义域为R，则实数m的取值范围为________．

答案：[0,1]

解析：依照m是否为零进行分类讨论．

(1)当m＝0时，f(x)＝，其定义域为R；

(2)当m≠0时，要使mx²－6mx+m+8≥0在x∈R的情况下均成立，必须满足

，解得0＜m≤1.

综合(1)、(2)可知m的取值范围为[0,1]．

11．已知函数f(x)是定义在x∈(－e,0)∪(0，e)上的奇函数，当x∈(－e,0)时，f(x)＝ax+ln(－x)，则当x∈(0，e)时，f(x)＝__________.

答案：ax－lnx

解析：当x∈(0，e)时，－x∈(－e,0)，f(x)＝－f(－x)＝－[a(－x)+lnx]＝ax－lnx，故填ax－lnx.

10．(2009·北京，12)已知函数f(x)＝若f(x)＝2，则x＝________.

答案：log₃2

解析：依题意得，当x≤1时，3^x＝2，∴x＝log₃2，

当x＞1时，－x＝2，x＝－2(舍去)，故x＝log₃2.

9．函数f(x)＝的定义域为________．

答案：[3，+∞)

解析：依题意，得，解之得x≥3.

8．(2011·原创题)设f(x)是定义域在R上的偶函数，它的图象关于直线x＝2对称，已知x∈[－2,2]时，函数f(x)＝－x²+1，则x∈[－6，－2]时，f(x)等于　　　　　　　　　　　　 (　)

A．－(x+4)²+1　 　　　　　　　　　　 B．－(x－4)²+1

C．－(x－4)²－1　 　　　　　　　　　　 D．－(x+4)²－1

答案：A

解析：∵f(x)是R上的偶函数，它的图象关于直线x＝2对称．

∴f(－x)＝f(x)，f(x+4)＝f(－x)∴f(x)＝f(x+4)．当x∈[－6，－2]时，x+4∈[－2,2]．

则f(x)＝f(x+4)＝－(x+4)²+1，故选A.