
题目列表(包括答案和解析)
1. (广东省深圳市2009 届高三九校联考数学试题)
下列说法错误的是 ( )
A. “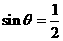 ”是“
”是“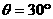 ”的充分不必要条件;
”的充分不必要条件;
B.命题“若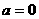 ,则
,则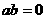 ”的否命题是:“若
”的否命题是:“若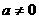 ,则
,则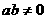 ”
”
C.若命题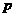 :
: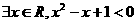 ,则
,则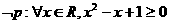 ;
;
D.如果命题“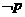 ”与命题“
”与命题“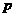 或
或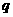 ”都是真命题,那么命题
”都是真命题,那么命题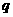 一定是真命题.
一定是真命题.
答案:A
9.(广东省四会中学2009届高三上学期第二次质量检测(数学理))
已知命题: P:对任意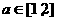 ,不等式
,不等式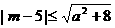 恒成立;
恒成立;
q:函数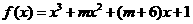 存在极大值和极小值。
存在极大值和极小值。
求使命题“p且 q”为真命题的m的取值范围。
q”为真命题的m的取值范围。
解: 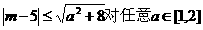 恒成立,
恒成立,
只需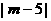 小于
小于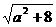 的最小值, 而当
的最小值, 而当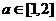 时,
时,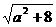 ≥3,
≥3,
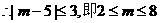 .
.
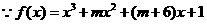 存在极大值与极小值,
存在极大值与极小值,
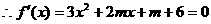 有两个不等的实根,
有两个不等的实根,
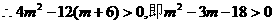 ,
,
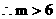 或
或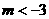 .
.
要使命题“p且 q”为真,只需
q”为真,只需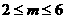 ,故m的取值范围为[2,6].
,故m的取值范围为[2,6].
★ 抢 分 频 道 ★
基础巩固训练
8.下列特称命题中假命题为( )
A. 空间中过直线外一点有且仅有一条直线与该直线垂直
B. 仅存在一个实数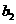 ,使得
,使得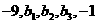 成等比数列
成等比数列
C. 存在实数 满足
满足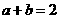 ,使得
,使得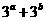 的最小值是6
的最小值是6
D. 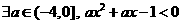 恒成立
恒成立
答案: A
考点三: 由命题真假确定参数范围
[例9] (广东省五校2009届高三上学期第二次联考(数学理))
已知命题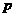 :方程
:方程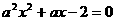 在
在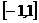 上有且仅有一解;命题
上有且仅有一解;命题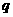 :只有一个实数
:只有一个实数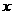 满足不等式
满足不等式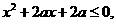 若命题
若命题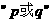 是假命题,求
是假命题,求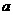 的取值范围.
的取值范围.
[解题思路]:因为命题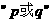 是假命题,由真值表可知,命题p和命题q都是假命题.由此入手分析。 注意参数的分类讨论,做到不重不漏。
是假命题,由真值表可知,命题p和命题q都是假命题.由此入手分析。 注意参数的分类讨论,做到不重不漏。
解析:由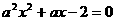 ,得
,得 显然
显然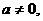
所以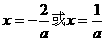 , 因为方程
, 因为方程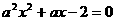 在
在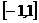 上有且仅有一解,故
上有且仅有一解,故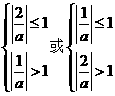 、
、
所以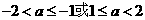 …
…
只有一个实数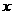 满足不等式
满足不等式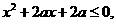 所以
所以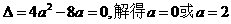
因为命题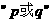 是假命题,所以命题p和命题q都是假命题.
是假命题,所以命题p和命题q都是假命题.
所以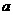 的取值范围为
的取值范围为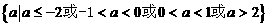
[名师指引]先确定简单命题与复合命题的真假,再由命题的真假划分参数的范围
[新题导练]
7.下列全称命题中真命题为( )
A. 一次函数都是单调函数 B. 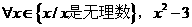 是有理数
是有理数
C. 任何一条直线都有斜率 D. 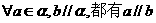
答案: A
6.设函数f(x)的定义域为R,有下列三个命题:
①若存在常数M,使得对任意x∈R,有f(x)≤M,则M是函数f(x)的最大值;
② 若存在x0∈R,使得对任意x∈R,且x≠x0,有f(x)<f(x0),则f(x0)是函数
f(x)的最大值;
③若存在x0∈R,使得对任意x∈R,有f(x)≤f(x0),则f(x0)是函数f(x)的最大值.
这些命题中,真命题的个数是
A.0 B.1 C.2 D.3
解:①错, 原因:可能“=”不能取到. ②③都正确,选C.
5.判断下列语句是不是命题,如果k,,,是,说明是全称命题还是特称命题.
(1) 中国的所有江河都流入太平洋;
(2)  不能作除数;
不能作除数;
(3) 有一个实数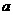 ,
,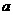 不能取对数;
不能取对数;
(4) 每一个向量都有方向吗?
解析:(1)(2)(3)是命题,(4)不是命题,其中(1)全称命题;(2)既不是全称命题也不是特称命题;(3)特称命题;
题型2: 判断全称命题或特称命题的真假
[例8] 设A、B为两个集合.下列四个命题:
①
A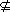 B
B 对任意x∈A,有x
对任意x∈A,有x B; ②A
B; ②A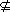 B
B A∩B=
A∩B=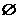 ; ③A
; ③A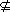 B
B A
A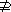 B;
B;
④ A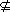 B
B 存在x∈A,使得x
存在x∈A,使得x B.
B.
其中真命题的序号是______________.(把符合要求的命题序号都填上)
[解题思路]:①要判定一个特称性命题为真,只要在给定的集合中,找到一个元素x,使命题p(x)为真;否则命题为假。②要判定一个全称命题为真,必须对给定的集合的每一个元素x,p(x)都为真;但要判断一个全称命题为假,只要在给定的集合内找出一个x0,p(x0)为假。
解析:A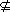 B
B 存在x∈A,有x
存在x∈A,有x B,故①错误;②错误;④正确. 亦或如下图所示.
B,故①错误;②错误;④正确. 亦或如下图所示.
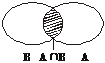
③A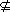 B
B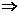 A
A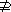 B不成立的反例如下图所示. 反之,同理.
B不成立的反例如下图所示. 反之,同理.
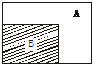
 真命题的序号是④
真命题的序号是④
[名师指引]判断全称命题与特称命题真假时,若判定一个特称性命题为真,只需找出一个例子即可否则命题为假;若判定一个全称命题为真,必须对每一个元素都为真;但判断其为假,只需要举出一个反例即可。
[新题导练]
4.(广东省四会中学2009届高三质量检测(数学理))
已知命题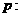 所有有理数都是实数,命题
所有有理数都是实数,命题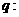 正数的对数都是负数,则下列命题中为真命题的是( )
正数的对数都是负数,则下列命题中为真命题的是( )
A.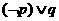 B.
B. C.
C.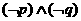 D.
D.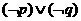
答案:D
考点二: 全称命题与特称命题及其真假判断
题型1: 判断命题是全称命题还是特称命题。
[例7] 判断下列语句是不是命题,如果k,,,是,说明是全称命题还是特称命题.
(1) 任何一个实数除以1,仍等于这个数;
(2) 三角函数都是周期函数吗?
(3) 有一个实数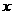 ,
,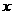 不能取倒数;
不能取倒数;
(4) 有的三角形内角和不等于
[解题思路]:含有全称量词的命题称为全称命题;含有存在量词的命题称为特称命题.但要注意有些命题可能省略了量词.
解析: (1)全称命题;(2)不是命题;(3)特称命题;(4)特称命题;
[名师指引]含有全称量词的命题称为全称命题;含有存在量词的命题称为特称命题.但要注意有些命题可能省略了量词.
[新题导练]
3. 分别指出由下列各组命题构成的逻辑关联词“或”、“且”、“非”的真假。
(1)p: 梯形有一组对边平行;q:梯形有一组对边相等。
(2)p: 1是方程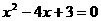 的解;q:3是方程
的解;q:3是方程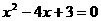 的解。
的解。
(3)p: 不等式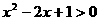 解集为R;q: 不等式
解集为R;q: 不等式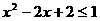 解集为
解集为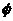 。
。
(4)p: 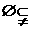
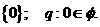
解:⑴
 p真,q假,
p真,q假,  “p
“p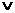 q”为真,“p
q”为真,“p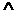 q”为假,“
q”为假,“ p”为假。
p”为假。
⑵
 p真,q真,
p真,q真,  “p
“p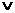 q”为真,“p
q”为真,“p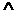 q”为真,“
q”为真,“ p”为假。
p”为假。
⑶  p假,q假,
p假,q假,  “p
“p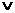 q”为假,“p
q”为假,“p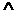 q”为假,“
q”为假,“ p”为真。
p”为真。
⑷  p真,q假,
p真,q假,  “p
“p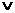 q”为真,“p
q”为真,“p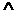 q”为假,“
q”为假,“ p”为假。
p”为假。
2.分别写出下列各组命题构成的“p或q”“p且q”“非p”形式的复合命题:
(1)p: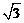 是无理数,q:
是无理数,q: 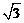 大于是2
大于是2
(2)p: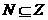 ,q:
,q: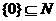
(3)p: 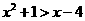 , q:
, q: 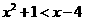
解: (1)p或q: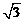 是无理数或大于2
是无理数或大于2
p且q: 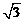 是无理数且大于2
是无理数且大于2
非p: 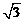 不是无理数
不是无理数
(2)p或q: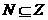 或
或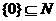
p且q: 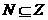 且
且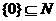
非p: 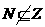
(3)p或q: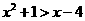 或
或 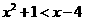
p且q: 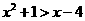 且
且 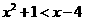
非p: 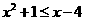
题型2。判断复合命题的真假
[例3] 写出由下述各命题构成的“p或q”,“p且q”,“非p”形式的复合命题,并指出所构成的这些复合命题的真假。
(1)p:5是17的约数,q:5是15的约数.
(2)p:方程x2-1=0的解是x=1, q:方程x2-1=0的解是x=-1,
(3)p:不等式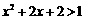 的解集为R,q:不等式
的解集为R,q:不等式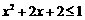 的解集为
的解集为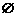
[解题思路]:写三种形式的复合命题时,在命题p或命题q的语句中,由于中文表达的习惯常常会有些省略,这种情况下应作词语上的调整。判断复合命题真假时,关键是判断简单命题的真假,再按真值表来判断即可.
解析:(1)p或q:5是17或15的约数;
p且q:5是17与15的公约数,(或写成:9是17的约数,且9是15的约数);
非p:5不是17的约数.
∵p假,q真,∴“p或q”为真,“p且q” 为假,而“非p”为真.
(2)p或q:方程x2-1=0的解是x=1,或方程x2-1=0的解是x=-1
(注意,不能写成“方程x2-1=0的解是x=±1”,这与真值表不符);
p且q:方程x2-1=0的解是x=1,且方程x2-1=0的解是x=-1;
非p:方程x2-1=0的解不都是x=1(注意,在命题p中的“是”应理解为“都是”的意思);
∵p假,q假,∴“p或q”与“p且q” 均为假,而“非p”为真.
(3)p或q:不等式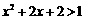 的解集为R或不等式
的解集为R或不等式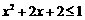 的解集为
的解集为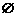 .
.
p且q:不等式 的解集为R或不等式
的解集为R或不等式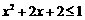 的解集为
的解集为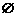
非p:不等式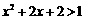 的解集为
的解集为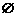 .
.
∵p真,q假,∴“p或q”为真,“p且q” 为假,而“非p”为假.
[例4] 已知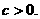 设P:函数
设P:函数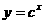 在R上单调递减; Q:不等式
在R上单调递减; Q:不等式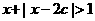 的解集为R,若“P或Q”是真命题,“P且Q”是假命题,求
的解集为R,若“P或Q”是真命题,“P且Q”是假命题,求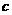 的取值范围.
的取值范围.
[解题思路]:“P或Q”是真命题,“P且Q”是假命题,根据真假表知,P,Q之中一真一假,因此有两种情况,要分类讨论.
解析:函数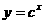 在R上单调递减
在R上单调递减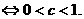
不等式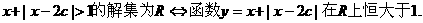
 [名师指引]先判断命题
[名师指引]先判断命题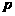 和
和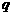 的真假,再根据真值表判断复合命题的真假.
的真假,再根据真值表判断复合命题的真假.
[新题导练]
1.分别指出下列复合命题的形式及构成它的简单命题:
(1)3是质数或合数.
(2)他是运动员兼教练员.
(3)相似三角形不一定是全等三角形.
解: (1) 这个命题是“p或q”形式,其中p:3是质数,q:3是合数.
(2) 这个命题是“p且q”形式,其中p:他是运动员,q:他是教练员.
(3) 这个命题是“非p”形式,其中p:相似三角形一定是全等三角形..
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com