1. □ABCD中，如果∠B=100°，那么∠A、∠D的值分别是 (　　 )

A.∠A=80°，∠D=100°　　　　 　B.∠A=100°，∠D=80°

C.∠B=80°，∠D=80°　　　　　 　D.∠A=100°，∠D=100°

10.是平行四边形,△AOE≌△COF.

11是平行四边形，四边形AMCN、BMDN是平行四边形.

9. 线段AC与EF互相平分.理由是：∵四边形ABCD是平行四边形.

∴AB∥CD,即AE∥CF，AB=CD，∵BE=DF，∴AE=CF

∴四边形AECF是平行四边形，

∴AC与EF互相平分.

8.证明：(1)∵BD=CD，∴∠BCD=∠1．∵ ∠l=∠2，∠BCD=∠2．∴CD∥AB．

　　 (2) ∵ CD∥AB　 ∴∠CDA=∠3．

　　　 ∠BCD=∠2=∠3．且BE=AE．且∠CDA=∠BCD．∴DE=CE．

　　　 在△BDE和△ACE中， DE=CE，∠DEB=∠CEA，BE=AE．∴△BDE≌△ACE

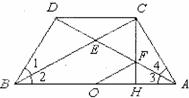　　 (3) ∵△BDE≌△ACE

　　　 ∠4=∠1，∠ACE=∠BDE=90°．

∴∠ACH=90°一∠BCH

　　　 又CH⊥AB，．∴ ∠2=90°一∠BCH

∴∠ACH=∠2=∠1=∠4．AF=CF

∵∠AEC=90°一∠4，∠ECF=90°一∠ACH

　　　 ∠ACH=∠4 ∠AEC=∠ECF．CF=EF．∴ EF=AF

　　　 O为AB中点，OF为△ABE的中位线　　 ∴OF=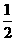BE

7.解：∵BA∥DE，BD∥AE，∴四边形ABDE是平行四边形

∴AB=DE，BD=AE，又EF=FC且AF∥BC，EC⊥BC，∴DE=DC，

∴EA+AE+EF=BD+DC+CF，∴二人同时到达F站.

6.证明：(1)∵ 四边形ABCD是平行四边形，∴AB∥CF．

　∴∠1=∠2，∠3=∠4　 ∵E是AD的中点，∴ AE=DE．

　∴△ABE ≌△DFE．

　(2)四边形ABDF是平行四边形．∵△ABE ≌△DFE　

∴AB=DF 又AB∥CF．∴四边形ABDF是平行四边形．

1.C;2.D，提示：根据三角形中位线的性质定理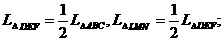：3.26或22，提示：当两腰上的中位线长为3时，则底边长为6，腰长为10，三角形的周长为26，当两腰上的中位线长为5时，则底边长为10，腰长为6，三角形的周长为22；4.平行四边形 ；5.平行四边形；

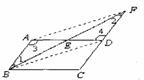
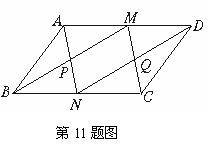
11.如图所示，平行四边形ABCD中，M、N分别为AD、BC的中点，连结AN、DN、BM、CM，且AN、BM交于点P，CM、DN交于点Q.四边形MGNP是平行四边形吗？为什么？

课时四答案：

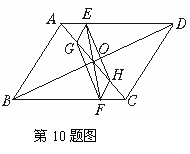
10. 如图所示，□ABCD的对角线AC、BD交于O，EF过点O交AD于E，交BC于F，G是OA的中点，H是OC的中点，四边形EGFH是平行四边形，说明理由.

9.. 已知如图：在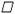ABCD中，延长AB到E，延长CD到F，使BE=DF，则线段AC与EF是否互相平分？说明理由.