
题目列表(包括答案和解析)
引题1:复数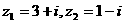 ,则
,则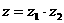 在复平面内的对应点位于( )
在复平面内的对应点位于( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限
小结:
引题2:计算:(1)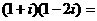 ;(2)
;(2)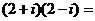 ;
;
(3)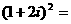 ;
;
小结:
引题3:计算: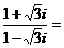 ;
;
小结:
2.一元二次方程的有关问题
掌握实系数一元二次方程的相关结论.
1. 复数代数形式的乘除运算
掌握复数代数形式的乘除运算及一些运算方法.
20、解:(Ⅰ)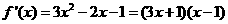 .
.
于是,当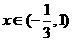 时,
时,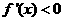 ;
;
当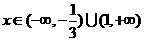 时,
时,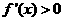 .
.
故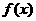 在
在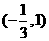 单调减少,在
单调减少,在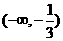 ,
,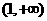 单调增加.
单调增加.
当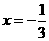 时,
时,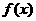 取得极大值
取得极大值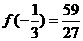 ;当
;当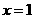 时,
时,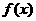 取得极小值
取得极小值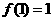 .
.
(Ⅱ)根据(Ⅰ)及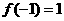 ,
,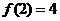 ,
,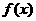 在
在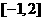 的最大值为4,最小值为1.
的最大值为4,最小值为1.
因此,当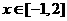 时,
时,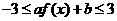 的充要条件是
的充要条件是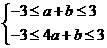 ,
,
即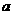 ,
,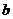 满足约束条件
满足约束条件
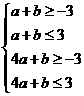 ,
,
由线性规划得,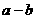 的最大值为7.
的最大值为7.
本资料由《七彩教育网》 提供!
19、解:(I)设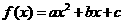 ,则
,则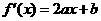 .
.
由题设可得: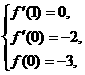 即
即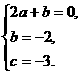 解得
解得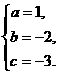
所以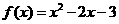 .
.
(II)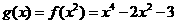 ,
,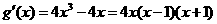 .
.
列表:
|
x |
(-∞,-1) |
-1 |
(-1,0) |
0 |
(0,1) |
1 |
(1,+∞) |
|
f¢(x) |
- |
0 |
+ |
0 |
- |
0 |
+ |
|
f(x) |
↘ |
|
↗ |
|
↘ |
|
↗ |
由表可得:函数g(x)的单调递增区间为(-1,0),(1,+∞).
18、.解:(1)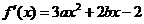 由条件知
由条件知
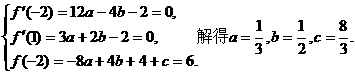
(2)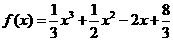 ,
,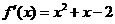
|
x |
-3 |
(-3,-2) |
-2 |
(-2,1) |
1 |
(1,3) |
3 |
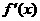 |
|
+ |
0 |
- |
0 |
+ |
|
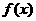 |
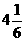 |
↗ |
6 |
↘ |
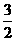 |
↗ |
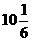 |
由上表知,在区间[-3,3]上,当x=3时,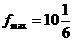 ,当x=1时,
,当x=1时,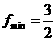 .
.
17、解:(Ⅰ)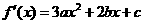 ,由已知
,由已知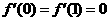 ,
,
即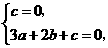 解得
解得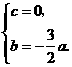
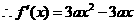 ,
,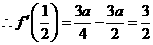 ,
,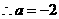 ,
,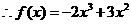 .
.
(Ⅱ)令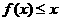 ,即
,即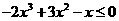 ,
,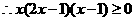 ,
,
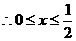 或
或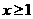 .又
.又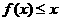 在区间
在区间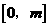 上恒成立,
上恒成立,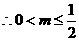 .
.
16、解:设该容器的高为xcm。容器的容积为ycm3。
依题意有y=(90-2x)(48-2x)x (0<x<24)
=4(x3-69x2+1080x)
∴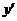 =4(3x2-138x+1080)=12(x-10)(x-36)=0
=4(3x2-138x+1080)=12(x-10)(x-36)=0
∴x=10 x=36(不合题意,舍去)
∴当高为10cm时,容器的容积最大,最大容积是19600cm3
15、解:∵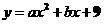 分别过(2,-1)点
分别过(2,-1)点
4a+2b+9=-1 (1)
又 y′=2ax+b ∴y′|x=2=4a+b=1 (2)
由(1)(2)可得,a=3,b=-11.
11、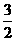 12、3 13、
12、3 13、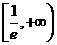 14、25
14、25
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com