
题目列表(包括答案和解析)
23.设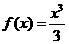 ,对任意实数
,对任意实数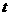 ,记
,记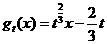 .
.
(I)求函数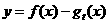 的单调区间;
的单调区间;
(II)求证:(ⅰ)当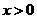 时,
时,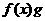
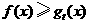 对任意正实数
对任意正实数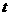 成立;
成立;
(ⅱ)有且仅有一个正实数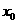 ,使得
,使得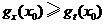 对任意正实数
对任意正实数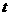 成立.
成立.
本题主要考查函数的基本性质,导数的应用及不等式的证明等基础知识,以及综合运用所学知识分析和解决问题的能力.满分15分.
22.设函数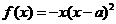 (
( ),其中
),其中 .
.
(Ⅰ)当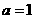 时,求曲线
时,求曲线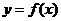 在点
在点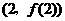 处的切线方程;
处的切线方程;
(Ⅱ)当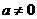 时,求函数
时,求函数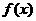 的极大值和极小值;
的极大值和极小值;
(Ⅲ)当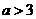 时,证明存在
时,证明存在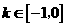 ,使得不等式
,使得不等式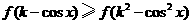 对任意的
对任意的 恒成立.
恒成立.
本小题主要考查运用导数研究函数的性质、曲线的切线方程,函数的极值、解不等式等基础知识,考查综合分析和解决问题的能力及分类讨论的思想方法.满分14分.
21.已知函数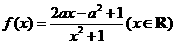 ,其中
,其中 .
.
(Ⅰ)当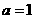 时,求曲线
时,求曲线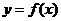 在点
在点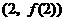 处的切线方程;
处的切线方程;
(Ⅱ)当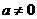 时,求函数
时,求函数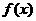 的单调区间与极值.
的单调区间与极值.
本小题考查导数的几何意义,两个函数的和、差、积、商的导数,利用导数研究函数的单调性和极值等基础知识,考查运算能力及分类讨论的思想方法.满分12分.
20.设函数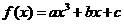
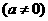 为奇函数,其图象在点
为奇函数,其图象在点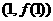 处的切线与直线
处的切线与直线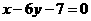 垂直,导函数
垂直,导函数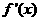 的最小值为
的最小值为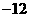 .
.
(Ⅰ)求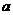 ,
,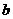 ,
,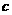 的值;
的值;
(Ⅱ)求函数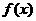 的单调递增区间,并求函数
的单调递增区间,并求函数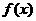 在
在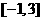 上的最大值和最小值.
上的最大值和最小值.
解析:本题考查函数的奇偶性、单调性、二次函数的最值、导数的应用等基础知识,以及推理能力和运算能力.
18.
解: (1)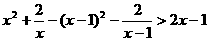 ,
,
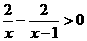 ,
,
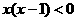 .
.
 原不等式的解为
原不等式的解为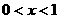 .
.
(2)当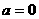 时,
时,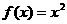 ,
,
对任意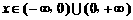 ,
,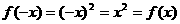 ,
,
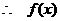 为偶函数.
为偶函数.
当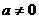 时,
时,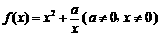 ,
,
取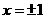 ,得
,得
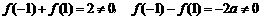 ,
,
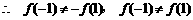 ,
,
 函数
函数 既不是奇函数,也不是偶函数.
19. (Ⅰ)解:展开式中二项式系数最大的项是第4项,这项是
既不是奇函数,也不是偶函数.
19. (Ⅰ)解:展开式中二项式系数最大的项是第4项,这项是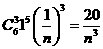
(Ⅱ)证法一:因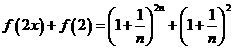
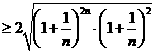
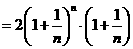
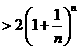
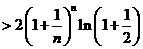
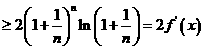
证法二:因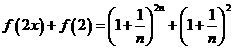
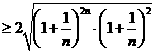
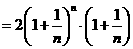
而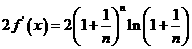
故只需对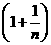 和
和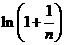 进行比较。
进行比较。
令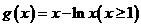 ,有
,有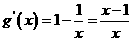
由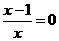 ,得
,得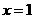
因为当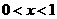 时,
时,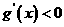 ,
,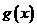 单调递减;当
单调递减;当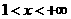 时,
时,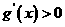 ,
,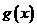 单调递增,所以在
单调递增,所以在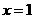 处
处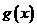 有极小值
有极小值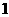
故当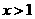 时,
时,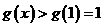 ,
,
从而有 ,亦即
,亦即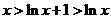
故有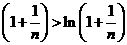 恒成立。
恒成立。
所以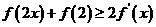 ,原不等式成立。
,原不等式成立。
(Ⅲ)对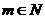 ,且
,且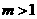
有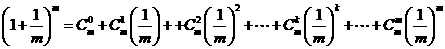
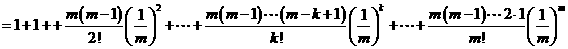
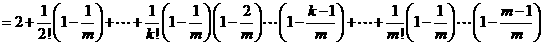
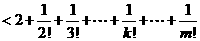
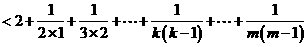
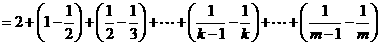
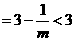
又因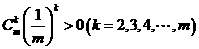 ,故
,故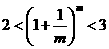
∵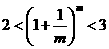 ,从而有
,从而有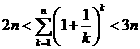 成立,
成立,
即存在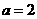 ,使得
,使得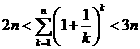 恒成立。
恒成立。
本资料由《七彩教育网》 提供!
17. 解:(1)当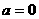 时,
时,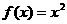 ,
,
对任意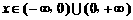 ,
,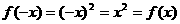 ,
,
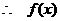 为偶函数.
为偶函数.
当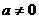 时,
时,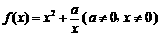 ,
,
取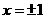 ,得
,得
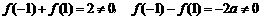 ,
,
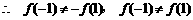 ,
,
 函数
函数 既不是奇函数,也不是偶函数.
既不是奇函数,也不是偶函数.
(2)解法一:设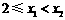 ,
,
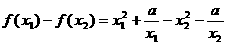
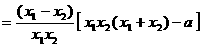 ,
,
要使函数 在
在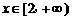 上为增函数,必须
上为增函数,必须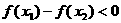 恒成立.
恒成立.
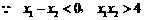 ,即
,即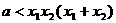 恒成立.
恒成立.
又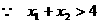 ,
,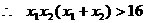 .
.
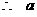 的取值范围是
的取值范围是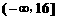 .
.
解法二:当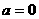 时,
时,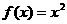 ,显然在
,显然在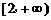 为增函数.
为增函数.
当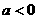 时,反比例函数
时,反比例函数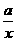 在
在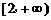 为增函数,
为增函数,
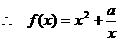 在
在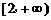 为增函数.
为增函数.
当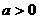 时,同解法一.
时,同解法一.
16. 解:(Ⅰ)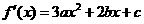 ,由已知
,由已知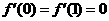 ,
,
即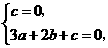 解得
解得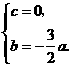
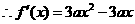 ,
,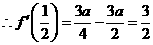 ,
,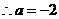 ,
,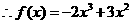 .
.
(Ⅱ)令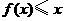 ,即
,即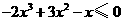 ,
,
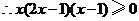 ,
,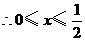 或
或 .
.
又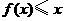 在区间
在区间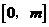 上恒成立,
上恒成立,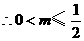 .
.
15. 解:(Ⅰ) 的定义域为
的定义域为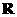 ,
,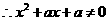 恒成立,
恒成立,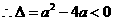 ,
,
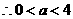 ,即当
,即当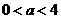 时
时 的定义域为
的定义域为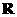 .
.
(Ⅱ)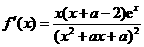 ,令
,令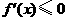 ,得
,得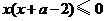 .
.
由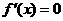 ,得
,得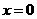 或
或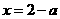 ,又
,又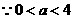 ,
,
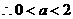 时,由
时,由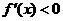 得
得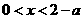 ;
;
当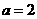 时,
时,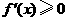 ;当
;当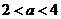 时,由
时,由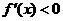 得
得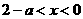 ,
,
即当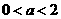 时,
时, 的单调减区间为
的单调减区间为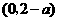 ;
;
当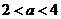 时,
时, 的单调减区间为
的单调减区间为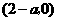 .
.
14. 证明:因为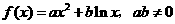 ,所以
,所以 的定义域为
的定义域为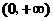 .
.
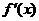
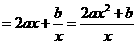 .
.
当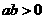 时,如果
时,如果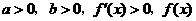 在
在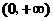 上单调递增;
上单调递增;
如果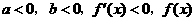 在
在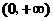 上单调递减.
上单调递减.
所以当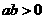 ,函数
,函数 没有极值点.
没有极值点.
当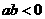 时,
时,
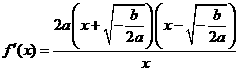
令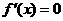 ,
,
将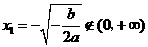 (舍去),
(舍去),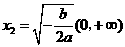 ,
,
当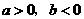 时,
时,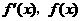 随
随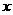 的变化情况如下表:
的变化情况如下表:
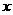 |
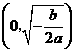 |
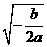 |
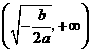 |
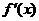 |
 |
0 |
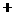 |
 |
 |
极小值 |
 |
从上表可看出,
函数 有且只有一个极小值点,极小值为
有且只有一个极小值点,极小值为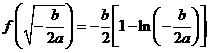 .
.
当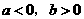 时,
时,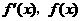 随
随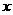 的变化情况如下表:
的变化情况如下表:
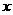 |
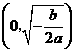 |
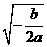 |
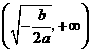 |
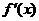 |
 |
0 |
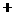 |
 |
 |
极大值 |
 |
从上表可看出,
函数 有且只有一个极大值点,极大值为
有且只有一个极大值点,极大值为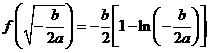 .
.
综上所述,
当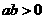 时,函数
时,函数 没有极值点;
没有极值点;
当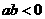 时,
时,
若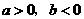 时,函数
时,函数 有且只有一个极小值点,极小值为
有且只有一个极小值点,极小值为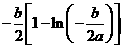 .
.
若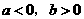 时,函数
时,函数 有且只有一个极大值点,极大值为
有且只有一个极大值点,极大值为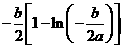 .
.
13. 解:(Ⅰ)由题意知, 的定义域为
的定义域为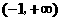 ,
,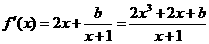
设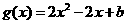 ,其图象的对称轴为
,其图象的对称轴为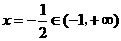 ,
,
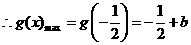 .
.
当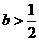 时,
时,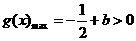 ,
,
即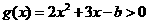 在
在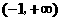 上恒成立,
上恒成立,
 当
当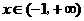 时,
时,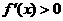 ,
,
 当
当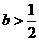 时,函数
时,函数 在定义域
在定义域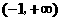 上单调递增.
上单调递增.
(Ⅱ)①由(Ⅰ)得,当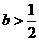 时,函数
时,函数 无极值点.
无极值点.
②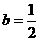 时,
时,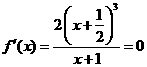 有两个相同的解
有两个相同的解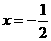 ,
,
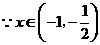 时,
时,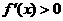 ,
,
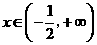 时,
时,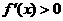 ,
,
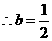 时,函数
时,函数 在
在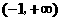 上无极值点.
上无极值点.
③当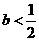 时,
时,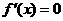 有两个不同解,
有两个不同解,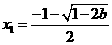 ,
,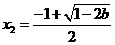 ,
,
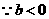 时,
时,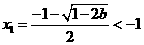 ,
,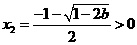 ,
,
即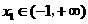 ,
,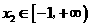 .
.
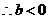 时,
时,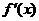 ,
, 随
随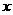 的变化情况如下表:
的变化情况如下表:
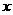 |
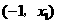 |
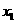 |
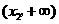 |
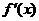 |
 |
 |
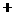 |
 |
 |
极小值 |
 |
由此表可知: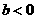 时,
时, 有惟一极小值点
有惟一极小值点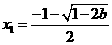 ,
,
当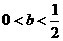 时,
时,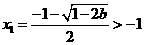 ,
,
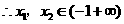 ,
,
此时,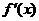 ,
, 随
随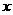 的变化情况如下表:
的变化情况如下表:
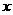 |
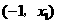 |
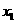 |
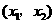 |
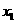 |
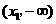 |
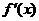 |
 |
 |
 |
 |
 |
 |
 |
极大值 |
 |
极小值 |
 |
由此表可知: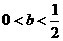 时,
时, 有一个极大值
有一个极大值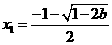 和一个极小值点
和一个极小值点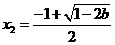 ;
;
综上所述:
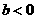 时,
时, 有惟一最小值点
有惟一最小值点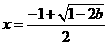 ;
;
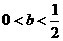 时,
时, 有一个极大值点
有一个极大值点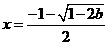 和一个极小值点
和一个极小值点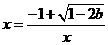 ;
;
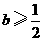 时,
时, 无极值点.
无极值点.
(Ⅲ)当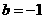 时,函数
时,函数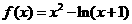 ,
,
令函数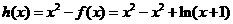 ,
,
则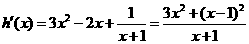 .
.
 当
当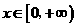 时,
时,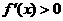 ,所以函数
,所以函数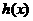 在
在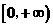 上单调递增,
上单调递增,
又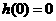 .
.
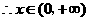 时,恒有
时,恒有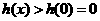 ,即
,即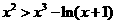 恒成立.
恒成立.
故当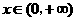 时,有
时,有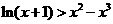 .
.
对任意正整数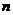 取
取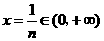 ,则有
,则有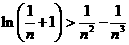 .
.
所以结论成立.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com