
题目列表(包括答案和解析)
2.(本小题满分12分)福建卷·文20)
已知函数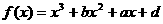 的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为
的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为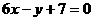 . (Ⅰ)求函数
. (Ⅰ)求函数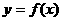 的解析式;(Ⅱ)求函数
的解析式;(Ⅱ)求函数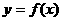 的单调区间.
的单调区间.
1.(本小题共13分)北京卷·理15文19)
已知函数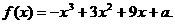
(Ⅰ)求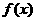 的单调减区间;
的单调减区间;
(Ⅱ)若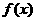 在区间[-2,2].上的最大值为20,求它在该区间上的最小值.
在区间[-2,2].上的最大值为20,求它在该区间上的最小值.
3.全国卷Ⅲ·文15)曲线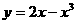 在点(1,1)处的切线方程为
. x+y-2=0
在点(1,1)处的切线方程为
. x+y-2=0
2.江苏卷14)曲线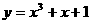 在点(1,3)处的切线方程是_____________________。
在点(1,3)处的切线方程是_____________________。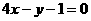
1.重庆卷·文12)曲线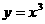 在点(1,1)处的切线与x轴、直线
在点(1,1)处的切线与x轴、直线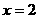 所围成的三角形的面积为
.
所围成的三角形的面积为
. 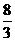
3.全国卷Ⅰ·文3)函数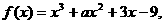 已知
已知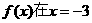 时取得极值,则a= ( B )
时取得极值,则a= ( B )
A.2 B.3 C.4 D.5
2.湖北卷·文11)在函数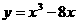 的图象上,其切线的倾斜角小于
的图象上,其切线的倾斜角小于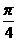 的点中,坐标为整数的点的个数是 ( D )
的点中,坐标为整数的点的个数是 ( D )
A.3 B.2 C.1 D.0
1.广东卷6)函数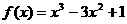 是减函数的区间为 ( D )
是减函数的区间为 ( D )
A.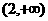 B.
B.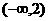 C.
C.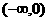 D.(0,2)
D.(0,2)
20、解:(Ⅰ)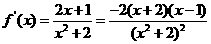 ,
,
当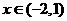 时,
时,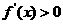 ;当
;当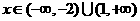 时,
时,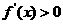 ;
;
故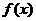 在
在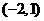 单调增加,在
单调增加,在 单调减少。
单调减少。
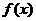 的极小值
的极小值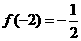 ,极大值
,极大值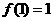
(Ⅱ)由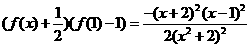 知
知
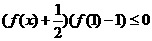 即
即 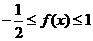
由此及(Ⅰ)知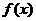 的最小值为
的最小值为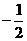 ,最大值为
,最大值为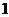
因此对一切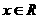 ,
,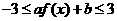 的充要条件是,
的充要条件是,
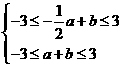
即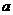 ,
,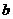 满足约束条件
满足约束条件
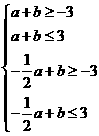 ,
,
由线性规划得,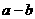 的最大值为5.
的最大值为5.
本资料由《七彩教育网》 提供!
19、解:(I)设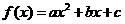 ,则
,则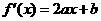 .
.
由题设可得: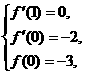 即
即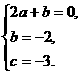 解得
解得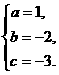
所以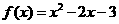 .
.
(II)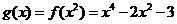 ,
,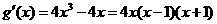 .
.
列表:
|
x |
(-∞,-1) |
-1 |
(-1,0) |
0 |
(0,1) |
1 |
(1,+∞) |
|
f¢(x) |
- |
0 |
+ |
0 |
- |
0 |
+ |
|
f(x) |
↘ |
|
↗ |
|
↘ |
|
↗ |
由表可得:函数g(x)的单调递增区间为(-1,0),(1,+∞).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com