
题目列表(包括答案和解析)
12. 解:求函数 的导数
的导数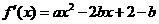 .
.
(Ⅰ)由函数 在
在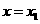 处取得极大值,在
处取得极大值,在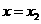 处取得极小值,知
处取得极小值,知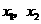 是
是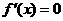 的两个根.
的两个根.
所以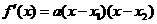
当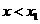 时,
时, 为增函数,
为增函数,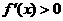 ,由
,由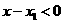 ,
,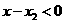 得
得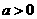 .
.
(Ⅱ)在题设下,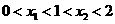 等价于
等价于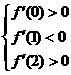 即
即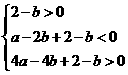 .
.
化简得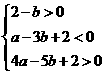 .
.
此不等式组表示的区域为平面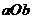 上三条直线:
上三条直线: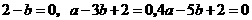 .
.
所围成的 的内部,其三个顶点分别为:
的内部,其三个顶点分别为: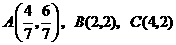 .
.
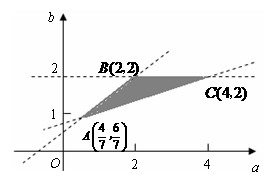
 在这三点的值依次为
在这三点的值依次为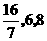 .
.
所以 的取值范围为
的取值范围为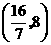 .
.
11. 解:(1)求函数 的导数;
的导数;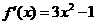 .
.
曲线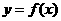 在点
在点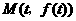 处的切线方程为:
处的切线方程为:
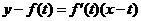 ,
,
即 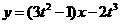 .
.
(2)如果有一条切线过点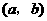 ,则存在
,则存在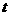 ,使
,使
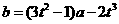 .
.
于是,若过点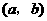 可作曲线
可作曲线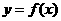 的三条切线,则方程
的三条切线,则方程
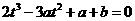
有三个相异的实数根.
记 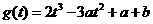 ,
,
则 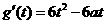
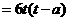 .
.
当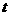 变化时,
变化时,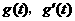 变化情况如下表:
变化情况如下表:
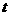 |
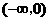 |
0 |
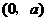 |
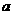 |
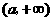 |
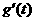 |
 |
0 |
 |
0 |
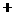 |
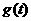 |
 |
极大值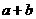 |
 |
极小值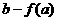 |
 |
由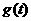 的单调性,当极大值
的单调性,当极大值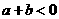 或极小值
或极小值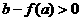 时,方程
时,方程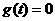 最多有一个实数根;
最多有一个实数根;
当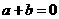 时,解方程
时,解方程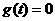 得
得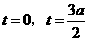 ,即方程
,即方程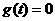 只有两个相异的实数根;
只有两个相异的实数根;
当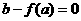 时,解方程
时,解方程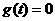 得
得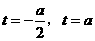 ,即方程
,即方程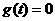 只有两个相异的实数根.
只有两个相异的实数根.
综上,如果过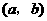 可作曲线
可作曲线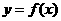 三条切线,即
三条切线,即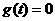 有三个相异的实数根,则
有三个相异的实数根,则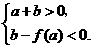
即 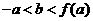 .
.
19.设函数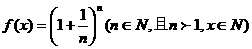 .
.
(Ⅰ)当x=6时,求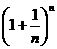 的展开式中二项式系数最大的项;
的展开式中二项式系数最大的项;
(Ⅱ)对任意的实数x,证明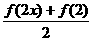 >
>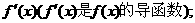
(Ⅲ)是否存在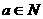 ,使得an<
,使得an<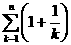 <
<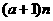 恒成立?若存在,试证明你的结论并求出a的值;若不存在,请说明理由.
恒成立?若存在,试证明你的结论并求出a的值;若不存在,请说明理由.
本题考察函数、不等式、导数、二项式定理、组合数计算公式等内容和数学思想方法。考查综合推理论证与分析解决问题的能力及创新意识。
答案解析
18.已知函数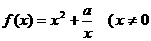 ,常数
,常数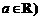 .
.
(1)当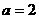 时,解不等式
时,解不等式 ;
;
(2)讨论函数 的奇偶性,并说明理由.
的奇偶性,并说明理由.
17. 已知函数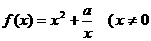 ,常数
,常数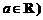 .
.
(1)讨论函数 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)若函数 在
在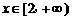 上为增函数,求
上为增函数,求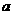 的取值范围.
的取值范围.
16.已知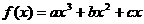 在区间[0,1]上是增函数,在区间
在区间[0,1]上是增函数,在区间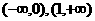 上是减函数,又
上是减函数,又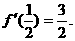
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)若在区间 (m>0)上恒有
(m>0)上恒有 ≤x成立,求m的取值范围.
≤x成立,求m的取值范围.
15.设函数f(x)=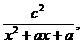 其中a为实数.
其中a为实数.
(Ⅰ)若f(x)的定义域为R,求a的取值范围;
(Ⅱ)当f(x)的定义域为R时,求f(x)的单减区间.
14.设函数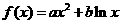 ,其中
,其中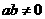 .
.
证明:当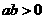 时,函数
时,函数 没有极值点;当
没有极值点;当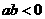 时,函数
时,函数 有且只有一个极值点,并求出极值.
有且只有一个极值点,并求出极值.
13.设函数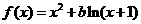 ,其中
,其中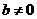 .
.
(Ⅰ)当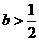 时,判断函数
时,判断函数 在定义域上的单调性;
在定义域上的单调性;
(Ⅱ)求函数 的极值点;
的极值点;
(Ⅲ)证明对任意的正整数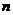 ,不等式
,不等式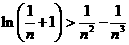 都成立.
都成立.
12.已知函数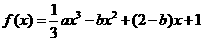
在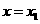 处取得极大值,在
处取得极大值,在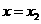 处取得极小值,且
处取得极小值,且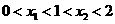 .
.
(1)证明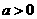 ;
;
(2)若z=a+2b,求z的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com