
题目列表(包括答案和解析)
3. 下列说法不正确的是______________
A. 空间中,一组对边平行且相等的四边形是一定是平行四边形;
B.同一平面的两条垂线一定共面;
C. 过直线上一点可以作无数条直线与这条直线垂直,且这些直线都在同一个平面内;
D. 过一条直线有且只有一个平面与已知平面垂直.
2.过点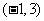 且平行于直线
且平行于直线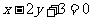 的直线方程为__________________
的直线方程为__________________
1. 已知直线经过点A(0,4)和点B(1,2),则直线AB的斜率为_________________
15已知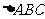 所在平面内一点
所在平面内一点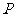 ,满足:
,满足: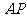 的中点为
的中点为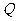 ,
,
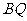 的中点为
的中点为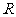 ,
,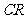 的中点为
的中点为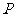 。设
。设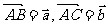 ,
,
如图,试用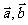 表示向量
表示向量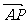 .
.
16已知关于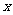 的方程
的方程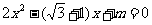 的两根为
的两根为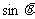 和
和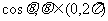 ,
,
(1)求实数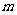 的值;
的值;
(2)求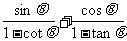 的值;(其中
的值;(其中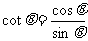 )
)
17四边形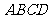 中,
中,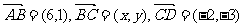
(1)若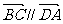 ,试求
,试求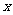 与
与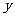 满足的关系式;
满足的关系式;
(2)满足(1)的同时又有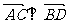 ,求
,求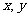 的值及四边形
的值及四边形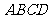 的面积。
的面积。
18某港口海水的深度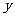 (米)是时间
(米)是时间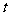 (时)(
(时)(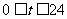 )的函数,记为:
)的函数,记为: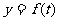
已知某日海水深度的数据如下:
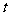 (时) (时) |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
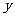 (米) (米) |
10.0 |
13.0 |
9.9 |
7.0 |
10.0 |
13.0 |
10.1 |
7.0 |
10.0 |
经长期观察,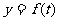 的曲线可近似地看成函数
的曲线可近似地看成函数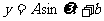 的图象
的图象
(1)试根据以上数据,求出函数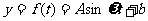 的振幅、最小正周期和表达式;
的振幅、最小正周期和表达式;
(2)一般情况下,船舶航行时,船底离海底的距离为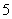 米或
米或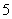 米以上时认为是安全的(船舶停靠时,船底只需不碰海底即可)。某船吃水深度(船底离水面的距离)为
米以上时认为是安全的(船舶停靠时,船底只需不碰海底即可)。某船吃水深度(船底离水面的距离)为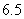 米,如果该船希望在同一天内安全进出港,请问,它至多能在港内停留多长时间(忽略进出港所需时间)?
米,如果该船希望在同一天内安全进出港,请问,它至多能在港内停留多长时间(忽略进出港所需时间)?
19已知向量
(1)求证: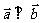 ;
;
(2)若存在不等于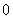 的实数
的实数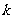 和
和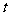 ,使
,使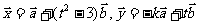 满足
满足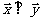 。试求此时
。试求此时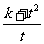 的最小值。
的最小值。
20.已知ΔABC的三个内角A、B.C满足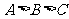 ,其中
,其中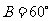 ,且
,且 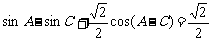 。
。
(1)求A、B.C的大小;
(2)求函数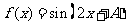 在区间
在区间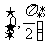 上的最大值与最小值
上的最大值与最小值
5.设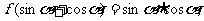 则
则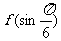 =_____________
=_____________
6若向量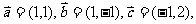 则
则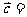 _________________(用
_________________(用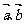 表示)
表示)
7函数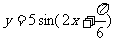 图象的对称轴方程是__________________
图象的对称轴方程是__________________
8已知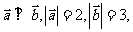 且
且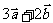 与
与 垂直,则实数
垂直,则实数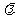 的值为________________
的值为________________
9函数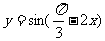 的单调递减区间是_____________________
的单调递减区间是_____________________
10有下列四种变换方式:
①向左平移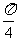 ,再将横坐标变为原来的
,再将横坐标变为原来的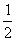 ; ②横坐标变为原来的
; ②横坐标变为原来的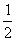 ,再向左平移
,再向左平移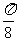 ;
;
③横坐标变为原来的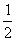 ,再向左平移
,再向左平移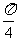 ;
④向左平移
;
④向左平移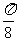 ,再将横坐标变为原来的
,再将横坐标变为原来的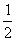 ;
;
其中能将正弦曲线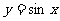 的图像变为
的图像变为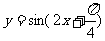 的图像的是______________
11
的图像的是______________
11 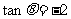 ,则
,则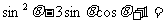
12已知点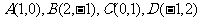 ,则
,则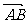 与
与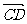 的夹角大小为______.
的夹角大小为______.
13已知正方形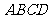 的边长为1,设
的边长为1,设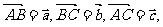 则
则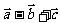 的模为 .
的模为 .
14函数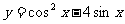 的值域是
的值域是
1化简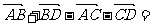 _________________
_________________
2 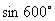 =_________________
=_________________
3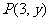 为
为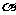 终边上一点,
终边上一点,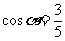 ,则
,则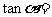 ______________
______________
4.已知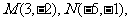 若
若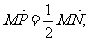 则
则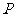 点的坐标为________________
点的坐标为________________
20、设各项均为正数的数列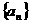 的前n项和为
的前n项和为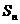 ,已知
,已知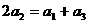 ,数列
,数列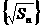 是公差为
是公差为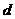 的等差数列.
的等差数列.
①求数列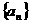 的通项公式(用
的通项公式(用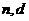 表示)
表示)
②设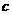 为实数,对满足
为实数,对满足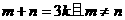 的任意正整数
的任意正整数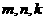 ,不等式
,不等式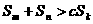 都成立。求证:
都成立。求证: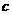 的最大值为
的最大值为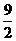
19、在某海滨城市附近海面有一台风,据测,当前台风中心位于城市O(如图)的东偏南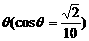 方向300km的海面P处,并以20km/h的速度向西偏北45°方向移动,台风侵袭的范围为圆形区域,当前半径为60km,并以10km/h
方向300km的海面P处,并以20km/h的速度向西偏北45°方向移动,台风侵袭的范围为圆形区域,当前半径为60km,并以10km/h
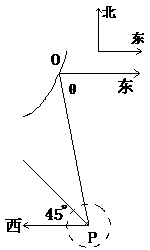 的速度不断增大,问几小时后该城市开始受到台风的侵袭?受到台风的侵袭的时间有多少小时?
的速度不断增大,问几小时后该城市开始受到台风的侵袭?受到台风的侵袭的时间有多少小时?
18、某兴趣小组测量电视塔AE的高度H(单位m),如示意图,垂直放置的标杆BC高度h=4m,仰角∠ABE=α,∠ADE=β
(1)该小组已经测得一组α、β的值,tanα=1.24,tanβ=1.20,,请据此算出H的值
(2)该小组分析若干测得的数据后,发现适当调整标杆到电视塔的距离d(单位m),使α与β之差较大,可以提高测量精确度,若电视塔实际高度为125m,问d为多少时,α-β最大
17、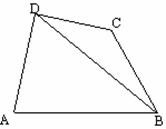 如图,在四边形ABCD中,已知AD^CD, AD=10, AB=14, ÐBDA=60°, ÐBCD=135° 求BC的长.
如图,在四边形ABCD中,已知AD^CD, AD=10, AB=14, ÐBDA=60°, ÐBCD=135° 求BC的长.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com