19．解：(1)该市逐年投入的电力型公交车的数量组成等比数列{a_n}，其中a₁＝128，q＝1．5，

则在2010年应该投入的电力型公交车为a₇＝a₁q⁶＝128×1．5⁶＝1458(辆)。

(2)记S_n＝a₁+a₂+…+a_n，依据题意，得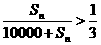。于是S_n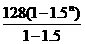＝>5000(辆)，即1．5ⁿ>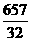，则有n≈7．5，因此n≥8。

∴到2011年底，电力型公交车的数量开始超过该市公交车总量的。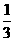

，，，

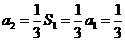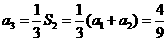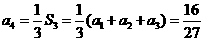由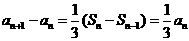(n≥2)，得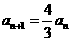(n≥2)，

又a₂=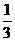，所以a_n=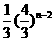(n≥2),

∴ 数列{a_n}的通项公式为；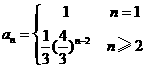

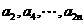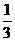(II)由(I)可知是首项为，公比为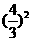项数为n的等比数列，∴ =.

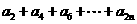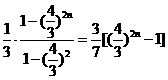18．解：⑴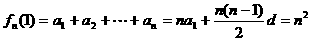

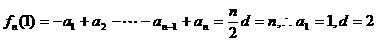，∴a_n＝2n－1(n∈N₊)

⑵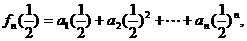∴通过差比数列求和可得：

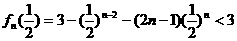，又可证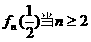时为单调递增函数。

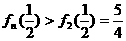∴，综上可证。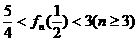

22．已知点P_n(a_n，b_n)都在直线L：y=2x+2上，P₁为直线L与x轴的交点，数列{a_n}成等差数列，公差为1(n∈N^＊)。

　　 ⑴求数列{a_n}，{b_n}的通项公式；

　　 ⑵若f(n)＝，问是否存在k∈N^＊，使得f(k+5)=2f(k)－2成立？若存在，求出k的值，若不存在，说明理由；

⑶求证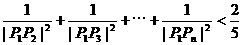：(n≥2，n∈N^＊)。

数列单元测试 (C卷)答案

21．某地区位于沙漠边缘地带，到2004年底该地区的绿化率只有30%，计划从2005年开始加大沙漠化改造的力度，每年原来沙漠面积的16% ，将被植树改造为绿洲，但同时原有绿洲面积的4%还会被沙漠化。

　　 ⑴设该地区的面积为1，2002年绿洲面积为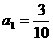，经过一年绿洲面积为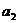……经过n年绿洲面积为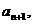求证：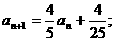

　　　 ⑵求证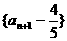：是等比数列；

　　　 ⑶问至少需要经过多少年努力，才能使该地区的绿洲面积超过60%？(取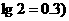

19．某市2003年共有1万辆燃油型公交车。有关部门计划于2004年投入128辆电力型公交车，随后电力型公交车每年的投入比上一年增加50%，试问：

⑴该市在2010年应该投入多少辆电力型公交车？

⑵到哪一年底，电力型公交车的数量开始超过该市公交车总量的？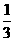

18．{a_n}是等差数列，设f_n(x)＝a₁x+a₂x²+…+a_nxⁿ，n是正偶数，且已知f_n(1)＝n²，f_n(－1)＝n。

　　　 ⑴求数列{a_n}的通项公式；

⑵证明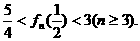

17．数列{a_n}的前n项和为S_n，且a₁=1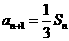，，n=1，2，3，……，求

　 (I)a₂，a₃，a₄的值及数列{a_n}的通项公式；

　 (II)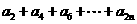的值.

16．在等差数列{a_n}中，当a_r＝a_s(r≠s)时，{a_n}必定是常数数列。然而在等比数列{a_n}中，对某些正整数r、s (r≠s)，当a_r＝a_s时，非常数数列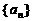的一个例子是____________．

15．已知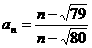(n∈N₊)，则在数列{a_n}的前50项中最大项的项数是　　。