5.+＝________.

[解析]　先配方，再结合根式的性质进行求解．

原式＝+

＝(1－)+|1－|＝1－+－1＝0.

[答案]　0

4．根据n次方根的意义，下列各式：①()ⁿ＝a；②不一定等于a；③n是奇数时，＝a；④n为偶数时，＝|a|.其中正确的有(　)

A．①②③④　 B．①③④

C．①②③　 　D．①②④

[解析]　按分数指数幂规定①②③④全正确．故选A.

[答案]　A

3.运算的结果是(　)

A．2　 B．－2

C．±2　 D．以上都不对

[解析]　＝＝2.故选A.

[答案]　A

2.+的值是(　)

A．0　 B．2(a－b)

C．0或2(a－b)　 D．a－b

[解析]　当a－b≥0时，

原式＝a－b+a－b＝2(a－b)；

当a－b<0时，原式＝b－a+a－b＝0.故选C.

[答案]　C

1．下列各式正确的是(　)

A.＝－4　　　B.＝m

C.＝3　 D．a⁰＝1

[解析]　根据根式的性质可知C正确．

＝|m|，a＝1条件为(a≠0)，故A、B、D错．

[答案]　C

22．(本小题满分14分)已知函数f(x)是定义在[－1,1]上的函数，若对于任意x，y∈[－1,1]，都有f(x+y)＝f(x)+f(y)，且x>0时，有f(x)>0.

(1)求f(0)的值；

(2)判断函数的奇偶性；

(3)判断函数f(x)在[－1,1]上是增函数还是减函数，并证明你的结论．

[解析]　(1)令x＝y＝0，则f(0+0)

＝f(0)+f(0)，

∴f(0)＝0

(2)令y＝－x，∴f(x－x)＝f(x)+f(－x)，

∴f(x)+f(－x)＝0，f(－x)＝－f(x)，

∴f(x)为奇函数．

(3)f(x)为增函数．

证明：令－1≤x₁<x₂≤1，∴x₂－x₁>0，

∴f(x₂－x₁)>0.

又∵f(x₂－x₁)＝f(x₂)+f(－x₁)

＝f(x₂)－f(x₁)，

∴f(x₂)－f(x₁)>0，∴f(x₂)>f(x₁)，

∴f(x)在[－1,1]上是增函数．

21．(本小题满分12分)已知x∈[－3,2]，求f(x)＝－+1的最小值．

[解析]　f(x)＝²－a×()^x+1

＝²+1－

令t＝()^x，x∈[－3,2]，则t∈[，8]

y＝(t－)²+1－，t∈[，8]

(1)当<，即a<时

t＝时y取最小值，

y_min＝－+1＝－.

(2)当≤≤8，即≤a≤16时，

t＝时y取最小值，y_min＝1－.

(3)当>8时即a>16时，t＝8时y取最小值，

y_min＝64－8a+1＝65－8a，

∴f(x)_min＝

20．(本小题满分12分)已知函数f(x)＝x^－1+x²－2，试利用基本初等函数的图象，判断f(x)有几个零点，并利用零点存在性定理确定各零点所在的区间(各区间长度不超过1)．

[解析]　

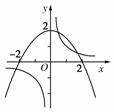
由f(x)=0，得x^-1=-1/2x²+2，令y1=x-1，y2=-1/2x²+2，

分别画出它们的图象如图，其中抛物线的顶点坐标为(0,2)，与x轴的交点为(-2,0)、(2,0)，y1与y2的图象有3个交点，从而函数f(x)有3个零点．

由f(x)的解析式知x≠0，f(x)的图象在(-∞，0)和(0，+∞) 　

19．(本小题满分12分)某公司今年1月份推出新产品A，其成本价为492元/件，经试销调查，销售量与销售价的关系如表：

由此可知，销售量y(件)与销售价x(元/件)可近似看作一次函数y＝kx+b的关系(通常取表中相距较远的两组数据所得的一次函数较为精确)．

试问：销售价定为多少时，1月份利润最大？并求最大利润和此时的销售量．

[解析]　由表可知⇒，

故y＝－x+1 000.

设1月份利润为W，则

W＝(x－492)(－x+1 000)

＝－x²+1 492x－492 000

＝－(x－746)²+64 516，

∴当x＝746时，W_max＝64 516，

此时销售量为1 000－746＝254(件)，

即当销售价定为746元/件时，1月份利润最大，最大利润为64 516元，此时销售量为254件．

18．(本小题满分12分)已知函数f(x)＝是奇函数，且f(1)＝2.

(1)求f(x)的解析式；

(2)判断函数f(x)在(0,1)上的单调性．

[解析]　∵f(x)是奇函数，∴f(－x)＝－f(x)

即＝－，

＝

比较系数得：c＝－c，∴c＝0

又∵f(1)＝2，∴＝2，b＝1

∴f(x)＝即f(x)＝x+.

(2)任取x₁，x₂∈(0,1)，且x₁<x₂

则f(x₁)－f(x₂)＝－

＝(x₁－x₂)

∵0<x₁<x₂<1.

∴x₁－x₂<0,1－<0

∴(x₁－x₂)>0即f(x₁)>f(x₂)．

f(x)在(0,1)上为减函数．