
题目列表(包括答案和解析)
4、若集合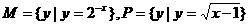 ,则
,则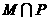 等于_____
等于_____
A、 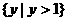 B、
B、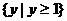 C、
C、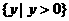 D、
D、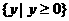
3、下列五个写法中①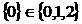 ,②
,②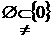 ,③
,③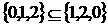 ,④
,④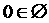 ,
,
⑤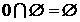 ,错误的写法个数是( )
,错误的写法个数是( )
A、1个 B、2个 C、3个 D、4个
2、若集合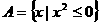 ,则下列结论中正确的是( )
,则下列结论中正确的是( )
A、A=0
B、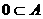 C、
C、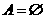 D、
D、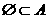
1、满足条件{1,2,3}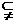 M
M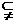 {1,2,3,4,5,6}的集合M的个数是 ( )
{1,2,3,4,5,6}的集合M的个数是 ( )
A、8 B、7 C、6 D、5
22.(本小题满分14分)设a>0,f(x)=+是R上的偶函数.
(1)求a的值;
(2)证明:f(x)在(0,+∞)上是增函数.
[解析] (1)解:∵f(x)=+是R上的偶函数,
∴f(x)-f(-x)=0.
∴+--=0,
即ex+e-x=0
(ex-e-x)=0.
由于ex-e-x不可能恒为0,
∴当-a=0时,式子恒成立.
又a>0,∴a=1.
(2)证明:∵由(1)知f(x)=ex+,
在(0,+∞)上任取x1<x2.
f(x1)-f(x2)=ex1+-ex2-
=(ex1-ex2)+(ex2-ex1)·.
∵e>1,∴0<ex1<ex2,ex1·ex2>1,
∴ex1+x2>1,(ex1-ex2)<0,
∴f(x1)-f(x2)<0,即f(x1)<f(x2),
∴f(x)在(0,+∞)上是增函数.
21.(本小题满分12分)已知函数f(x)=lg(1+x)-lg(1-x).
(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性;
[解析] (1)由得-1<x<1,
∴函数f(x)的定义域为(-1,1).
(2)定义域关于原点对称,对于任意的x∈(-1,1),
有-x∈(-1,1),
f(-x)=lg(1-x)-lg(1+x)=-f(x)
∴f(x)为奇函数.
20.(本小题满分12分)有一批影碟机(VCD)原销售价为每台800元,在甲、乙两家商场均有销售,甲商场用下面的方法促销:买一台单价为780元,买两台单价为760元,依次类推,每多买一台单价均减少20元,但每台最低不低于440元;乙商场一律按原价的75%销售,某单位需购买一批此类影碟机,问去哪家商场购买花费较少?
[解析] 设购买x台,甲、乙两商场的差价为y,则去甲商场购买共花费(800-20x)x,由题意800-20x≥440.
∴1≤x≤18(x∈N).
去乙商场花费800×75%x(x∈N*).
∴当1≤x≤18(x∈N*)时
y=(800-20x)x-600x=200x-20x2,
当x>18(x∈N*)时,y=440x-600x=-160x,
则当y>0时,1≤x≤10;
当y=0时,x=10;
当y<0时,x>10(x∈N).
综上可知,若买少于10台,去乙商场花费较少;若买10台,甲、乙商场花费相同;若买超过10台,则去甲商场花费较少.
19.(本小题满分12分)(1)计算:+(lg5)0+()-;
(2)解方程:log3(6x-9)=3.
[解析] (1)原式
=+(lg5)0+-
=+1+=4.
(2)由方程log3(6x-9)=3得
6x-9=33=27,∴6x=36=62,∴x=2.
经检验,x=2是原方程的解.
18.(本小题满分12分)已知函数f(x)=x2+2ax+2,x∈[-5,5].
(1)当a=-1时,求f(x)的最大值和最小值;
(2)求实数a的取值范围,使y=f(x)在区间[-5,5]上是单调函数.
[解析] (1)当a=-1时,
f(x)=x2-2x+2=(x-1)2+1,x∈[-5,5].
由于f(x)的对称轴为x=1,结合图象知,
当x=1时,f(x)的最小值为1,
当x=-5时,f(x)的最大值为37.
(2)函数f(x)=(x+a)2+2-a2的图象的对称轴为x=-a,
∵f(x)在区间[-5,5]上是单调函数,
∴-a≤-5或-a≥5.
故a的取值范围是a≤-5或a≥5.
17.(本小题满分12分)已知函数f(x)=x2-3x-10的两个零点为x1,x2(x1<x2),设A={x|x≤x1,或x≥x2},B={x|2m-1<x<3m+2},且A∩B=Ø,求实数m的取值范围.
[解析] A={x|x≤-2,或x≥5}.
要使A∩B=Ø,必有
或3m+2<2m-1,
解得或m<-3,即-≤m≤1,或m<-3.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com