
题目列表(包括答案和解析)
3. 对于下列四个命题:①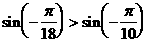 ;②
;②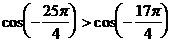 ;③
;③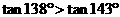 ;④
;④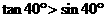 。其中正确命题的序号是( )
。其中正确命题的序号是( )
A. ①③ B. ①④ C. ②③ D. ②④
2. 求值: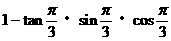 等于( )
等于( )
A. 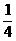 B.
B.
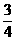 C.
C.
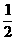 D.
D.
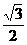
1. 若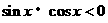 ,则角x的终边位于( )
,则角x的终边位于( )
A. 第二、四象限 B. 第二、三象限
C. 第一、二象限 D. 第三、四象限
22.在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O,如图5-6的东偏南θ(θ=arccos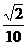 )方向300 km海平面P处,并以20 km/h的速度向西偏北45°方向移动,台风侵袭区域为圆形,当前半径为600 km,并以10 km/h的速度不断增大,问:几小时后该城市开始受到台风侵袭.
)方向300 km海平面P处,并以20 km/h的速度向西偏北45°方向移动,台风侵袭区域为圆形,当前半径为600 km,并以10 km/h的速度不断增大,问:几小时后该城市开始受到台风侵袭.
解:如图5-7,设t时刻台风中心为Q,此时台风侵袭的圆形区域半径为(10t+60) km,若在t时刻城市O受到台风侵袭则OQ≤10t+60.
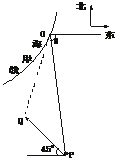
图5-7
由余弦定理,知
OQ2=PQ2+PO2-2PQ·POcosOPQ.
由于PO=300,PQ=20t,
cosOPQ=cos(θ-45°)
=cosθcos45°+sinθsin45°
=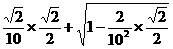 =
=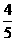 .
.
故OQ2=(20t)2+3002-2×20t×300×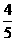
=202t2-9600t+3002.
因此,202t2-9600t+3002≤(10t+60)2,即t2-36t+288≤0.
∴(t-12)(t-24)≤0.∴12≤t≤24.
故经过12小时后,台风开始袭击该城市.??
21.已知A、B是△ABC的两个内角,i、j是互相垂直的单位向量,m=cos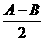 i+
i+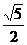 sin
sin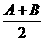 j,若|m|=
j,若|m|=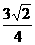 ,试求tanA·tanB.
,试求tanA·tanB.
解:∵i·j=0,|i|=|j|=1,
∴|m|2=m2=cos2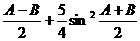
=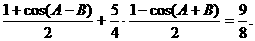
∴4cos(A-B)=5cos(A+B),
4cosAcosB+4sinAsinB=5cosAcosB-5sinAsinB.
∴9sinA·sinB=cosA·cosB.又△ABC中,sinA·sinB≠0,
∴cosA·cosB≠0.∴tanA·tanB=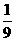 .
.
20.经过△ABO的重心G的直线与OA、OB两边分别交于P、Q两点,设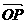 =m
=m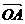 ,
,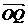 =n·
=n·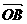 ,求
,求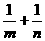 的值.
的值.
解:设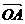 =a,
=a,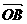 =b,则
=b,则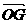 =
=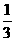 (a+b),
(a+b),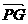 =
=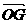 -
-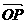 =
=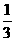 (a+b)-ma=(
(a+b)-ma=(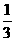 -m)a+
-m)a+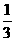 b.因P、G、Q三点共线,所以存在实数λ,使
b.因P、G、Q三点共线,所以存在实数λ,使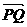 =λ
=λ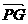 ,即nb-ma=λ
,即nb-ma=λ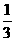 [(-m)a+
[(-m)a+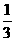 b].于是有
b].于是有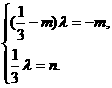
消去λ,得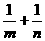 =3.
=3.
19.在△ABC中,已知A>B>C,且A=2C,A、B、C所对的边分别为a、b、c,b=4.又a、b、c成等差数列,求a、c的长.
解:由正弦定理得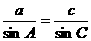 ,又A=2C,∴
,又A=2C,∴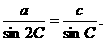
∴cosC=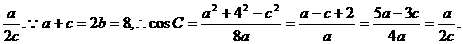
可得2a=3c,与a+c=8联立,解得a=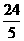 ,c=
,c=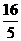 .
.
18.非零向量a和b满足|a|=|b|=|a-b|,求a与(a+b)的夹角.
解:设a与(a+b)的夹角为θ,由|a|=|b|=|a-b|,得
|a|2=|b|2=|a-b|2=|a|2+|b|2-2a·b,故a·b=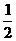 |a|2.
|a|2.
而|a+b|2=|a|2+|b|2+2a·b=3|a|2,∴|a+b|=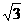 a.
a.
因此,cosθ=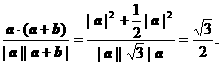
又0°≤θ≤180°,故θ=30°.
17.设两个非零向量e1和e2不共线,如果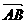 =e1+e2,
=e1+e2,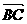 =2e1+8e2,CD=3(e1-e2).
=2e1+8e2,CD=3(e1-e2).
(1)求证:A、B、D三点共线;
(2)试确定实数k的值,使ke1+e2和e1+ke2共线.
(1)证明:∵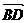 =
=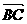 +
+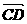 =5e1+5e2=5
=5e1+5e2=5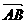 ,
,
∴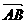 与
与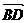 共线.又B为公共点,∴A、B、D三点共线.
共线.又B为公共点,∴A、B、D三点共线.
(2)解:∵ke1+e2=λ(e1+ke2),∴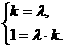
解得k=±1.
16.设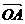 =(-2,m),
=(-2,m),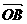 =(n,1),
=(n,1),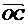 =(5,-1),若A、B、C三点共线,且OA⊥OB,则m+n的值是___________.
=(5,-1),若A、B、C三点共线,且OA⊥OB,则m+n的值是___________.
答案:9或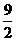
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com