5．用区间表示下列数集：

(1){x|x≥1}＝________.

(2){x|2<x≤4}＝________.

(3){x|x>－1且x≠2}＝________.

[答案]　(1)[1，+∞)　(2)(2,4]　(3)(－1,2)∪(2，+∞)

4．已知函数f(x)＝，则f(2)等于(　)

A．3　 B．2

C．1　 D．0

[解析]　f(2)＝＝3.故选A.

[答案]　A

3．下列各组函数表示相等函数的是(　)

A．y＝与y＝x+2

B．y＝－1与y＝x－1

C．y＝(x⁰－1)⁰(x≠1)与y＝1(x≠1)

D．y＝2x+1，x∈Z与y＝2x－1，x∈Z

[解析]　A组中两函数定义域不同，B、D中两函数的对应关系不同，C组中定义域与对应关系均相同，故选C.

[答案]　C

2．函数y＝ 的定义域是(　)

A．[－1，+∞)　　　B．[－1,0)

C．(－1，+∞)　 D．(－1,0)

[解析]　要使函数式有意义，须满足x+1＞0，

∴x＞－1.故定义域为(－1，+∞)．故选C.

[答案]　C

1．下列式子中不能表示函数y＝f(x)的是(　)

A．x＝y²+1　 B．y＝2x²+1

C．x－2y＝6　 D．x＝

[解析]　对于A，

由x＝y²+1得y²＝x－1.

￥资%源~网当x＝5时，

y＝±2，故y不是x的函数；

对B，y＝2x²+1是二次函数；

对C，x－2y＝6⇒y＝x－3是一次函数；

对D，由x＝得y＝x²(x≥0)是二次函数．故选A.

[答案]　A

9．(10分)某市出租车的计价标准是：4 km以内10元，超过4 km且不超过18 km的部分1.2元/km，超过18 km的部分1.8元/km.

(1)如果不计等待时间的费用，建立车费与行车里程的函数关系式；

(2)如果某人乘车行驶了20 km，他要付多少车费？

[解析]　(1)设车费为y元，行车里程为x km，则根据题意得

y＝

(2)当x＝20时，

y＝1.8×20－5.6＝30.4，

即当乘车20 km时，要付30.4 元车费．

8．已知函数f(x)＝x²+2x+a，f(bx)＝9x²－6x+2，其中x∈R，a，b为常数，求方程

f(ax+b)＝0的解集．

[解析]　∵f(x)＝x²+2x+a，

∴f(bx)＝(bx)²+2(bx)+a＝b²x²+2bx+a.

又∵f(bx)＝9x²－6x+2，

∴b²x²+2bx+a＝9x²－6x+2

即(b²－9)x²+2(b+3)x+a－2＝0.

∵x∈R，∴，即，

∴f(ax+b)＝f(2x－3)＝(2x－3)²+2(2x－3)+2

＝4x²－8x+5＝0.

∵Δ＝(－8)²－4×4×5＝－16＜0，

∴f(ax+b)＝0的解集是Ø.

[答案]　Ø

7．已知函数f(x)的图象是两条线段(如图，不含端点)，求f.

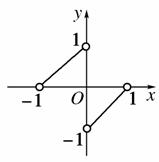
[解析]　由图象知

f(x)＝，

∴f＝－1＝－，

∴f＝f＝－+1＝

6．已知f(x)与g(x)分别由下表给出

那么f(g(3))＝________.

[解析]　由表知g(3)＝4，f(g(3))＝f(4)＝1.

[答案]　1

5．函数f(x)＝x²－4x+2，x∈[－4,4]的最小值是________，最大值是________．

[解析]　f(x)＝(x－2)²－2，作出其在[－4,4]上的图象知

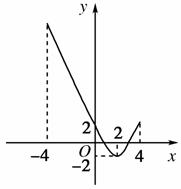
f(x)min=f(2)=-2；

f(x)max=f(-4)=34.

[答案]　-2,34