
题目列表(包括答案和解析)
7.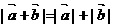 (
(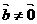 )成立的充要条件是
(
)
)成立的充要条件是
(
)
A.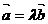 (
(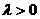 )
B.
)
B.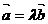 (
(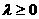 )
)
C.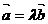 (
(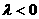 )
D.以上均不正确.
)
D.以上均不正确.
6.已知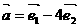 ,
,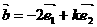 ,且
,且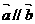 ,则
,则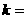 ( )
( )
A.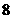 B.
B.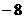 C.
C.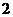 D.
D.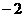 .
.
5.已知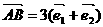 ,
,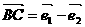 ,
,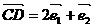 .则下列关系一定
.则下列关系一定
成立的是( )
A.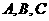 三点共线
B.
三点共线
B.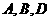 三点共线
三点共线
C.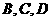 三点共线
D.
三点共线
D.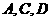 三点共线.
三点共线.
4.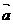 ,
,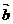 共线是
共线是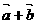 与
与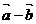 共线的
(
)
共线的
(
)
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件.
3.在平行四边形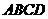 中,设
中,设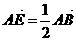 ,记
,记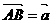 ,
,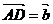 ,
,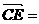 (
)
(
)
A.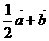 B.
B.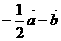 C.
C.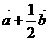 D.
D.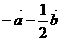 .
.
2.已知点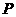 分有向线段
分有向线段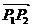 的比是
的比是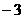 ,则
,则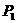 分
分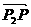 所成的比是( )
所成的比是( )
A.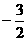 B.
B.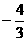 C.
C.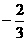 D.
D.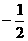 .
.
1.下列命题:(1)时间、速度、加速度都是向量;(2)向量的模是一个非负实数;(3)所有的单位向量都相等;(4)共线向量一定在同一条直线上.其中真命题的个数为 ( )
A.0个 B.1个 C.2个 D.3个.
(15) 本题主要考查向量共线的充要条件.
解:(1)∵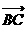 =2
=2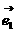 +8
+8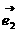 ,
,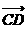 =3(
=3(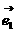 -
-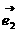 )
)
∴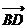 =
=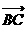 +
+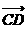 =2
=2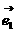 +8
+8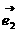 +3(
+3(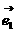 -
-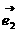 )=5(
)=5(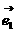 +
+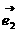 )=5
)=5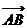
∴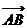 和
和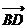 共线, 又
共线, 又 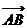 和
和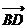 有公共点
有公共点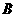
∴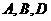 三点共线
三点共线
(2)∵k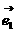 +
+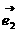 与
与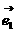 +k
+k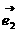 共线
共线
∴存在实数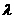 ,使k
,使k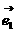 +
+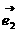 =
=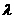 (
(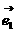 +k
+k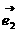 )
)
即(k-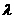 )
)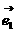 +(1-k
+(1-k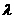 )
)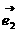 =
=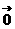 ∵向量
∵向量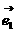 ,
,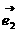 不共线
不共线
∴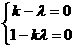 解得:k=±1
解得:k=±1
∴ 当k=±1时,k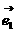 +
+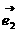 与
与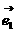 +k
+k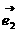 共线
共线
(16) 本题主要考查向量的表示以及向量平行和垂直的充要条件的运用.
解: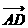 =
=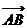 +
+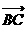 +
+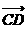 =(x+4)
=(x+4)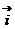 +(y-2)
+(y-2)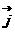
又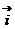 ,
,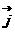 分别是x,y轴方向上的单位向量
分别是x,y轴方向上的单位向量
∴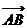 =(6,1),
=(6,1),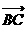 =(x,y),
=(x,y),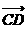 =(-2,-3),
=(-2,-3),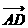 =(x+4,y-2)
=(x+4,y-2)
∵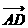 ‖
‖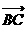 ∴(x+4)y-x(y-2)=0 即 x+2y=0
①
∴(x+4)y-x(y-2)=0 即 x+2y=0
①
又 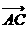 =
=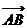 +
+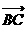 =(x+6,y+1),
=(x+6,y+1),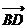 =
=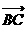 +
+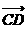 =(x-2,y-3)
=(x-2,y-3)
且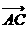
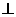
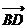 ∴
∴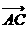 ·
·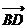 =0 从而得 (x+6)(x-2)+(y+1)(y-3)=0 ②
=0 从而得 (x+6)(x-2)+(y+1)(y-3)=0 ②
由①,②解得x=2,y=-1或x=-6,y=3
(17)本题主要考查综合运用正弦定理、余弦定理以及三角形面积公式解三角形和判断三角形形状.
解:(1)由题设,易知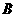 =60°,且a>b>c
=60°,且a>b>c
∵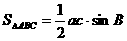 =
=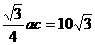 ∴ ac=40 ①
∴ ac=40 ①
又 a+c=13 ② 由 ①②解得: a=8,c=5 或a=5,c=8(舍去)
又由余弦定理得: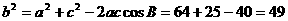
∴ b=7 ∴ △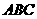 的三边长为8,7,5.
的三边长为8,7,5.
(2)由正弦定理得:2Rsin =a,2Rsin
=a,2Rsin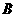 =b,
=b,
∴ 2Rsin cos
cos =2Rsin
=2Rsin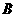 cos
cos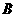 即 sin2
即 sin2 = sin2
= sin2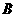
由已知 ,
,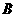 为三角形内角, ∴
为三角形内角, ∴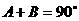 或
或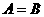
∴△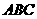 为直角三角形或等腰三角形.
为直角三角形或等腰三角形.
(18)本题主要考查向量的模、向量的数量积的概念,向量平行和垂直的充要条件的运用.
解:(1)设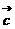 =(x,y)
=(x,y)
∵ |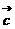 |=2
|=2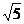 ∴
∴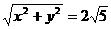 即
即
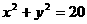 ①
①
又∵ 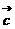 ‖
‖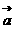 ,
,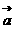 =(1,2)
∴2x-y=0 ②
=(1,2)
∴2x-y=0 ②
由 ①②得:x=2,y=4 或 x=-2,y=-4
∴ 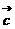 =(2,4)或
=(2,4)或 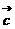 =(-2,-4)
=(-2,-4)
(2)∵ (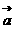 +2
+2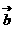 )
)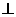 ( 2
( 2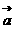 -
-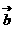 ) ∴(
) ∴(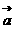 +2
+2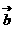 )·( 2
)·( 2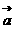 -
-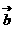 )=0
)=0
即 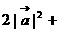 3
3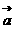 ·
·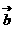 -2|
-2|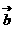 |²=0
|²=0
∴ 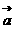 ·
·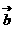 =-
=-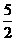 又|
又|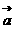 |=
|=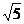 ,|
,|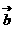 |=
|=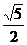
∴ cos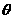 =
=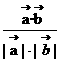 =-1
∵
=-1
∵ 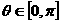 ∴
∴ 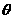 =
=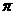
(19) 解:(1)设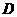 点坐标为(x,y),
点坐标为(x,y),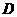 分
分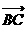 所成的比为
所成的比为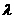 ,则
,则
x=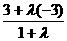 , y=
, y=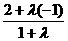
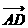 =(
=( 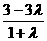 -2,
-2,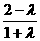 +1) ,
+1) ,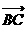 =(-6,-3)
=(-6,-3)
∵ 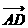
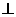
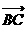 ∴
∴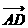 ·
·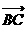 =0 ∴
-6(
=0 ∴
-6(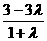 -2)-3(
-2)-3(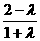 +1)=0 解得
+1)=0 解得 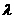 =
=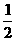 ∴
x=1 ,y=1
∴
x=1 ,y=1
故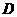 点坐标为(1,1),
点坐标为(1,1),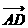 =(-1,2)
=(-1,2)
另解:设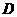 点坐标为(x,y),AD是BC边上的高,
点坐标为(x,y),AD是BC边上的高,
∴ 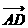
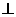
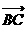 ,
,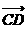 与
与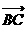 共线
共线
又∵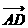 =(x
=(x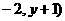
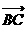 =(-6,-3)
=(-6,-3) 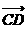 =(x+3,y+!)
=(x+3,y+!)
∴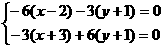 解得:x=1 ,y=1
解得:x=1 ,y=1
故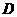 点坐标为(1,1),
点坐标为(1,1),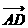 =(-1,2)
=(-1,2)
(2)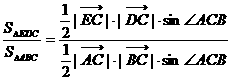 =
=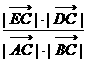 =
=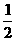
由(1)知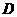 分
分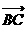 所成的比为
所成的比为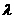 =
=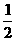 , ∴
, ∴ 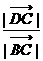 =
=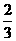
∴ 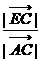 =
=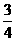 ∴
∴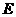 分
分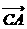 所成的比为3
所成的比为3
由定比分点坐标公式得: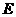 点坐标为(
点坐标为(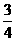 ,-1)
,-1)
(20) 解:由三角形面积公式得m=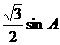 ,n=
,n=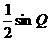
(1) 若 、
、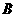 、
、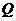 、
、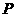 四点共圆,则
四点共圆,则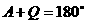
∴
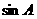 =
=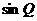 ∴
∴  ²+
²+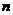 ²=
²=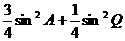 =sin²
=sin²
由余弦定理,在△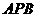 中,
中,
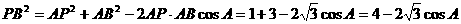 在△
在△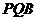 中,
中,
 ∴
∴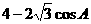 =
=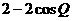 ∵cos
∵cos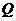 =-cos
=-cos
∴cos =
=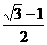 cos²
cos² =1-
=1-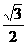
∴ ²+
²+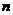 ²=sin²
²=sin² =1- cos²
=1- cos² =
=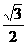
(2) ²+
²+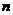 ²=
²=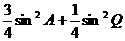
由余弦定理得: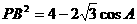
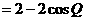
∴ 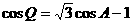
∴ ²+
²+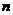 ²=
²=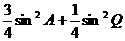 =
=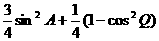
=
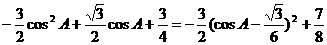
由条件可知0< <90°(当
<90°(当
 90°时,
90°时,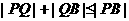 矛盾)
矛盾)
∴  <cos
<cos <1
<1
从而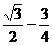 <
< ²+
²+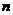 ²<
²<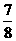
(11) 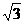 (12)y=-cos2x+3 (13)
(12)y=-cos2x+3 (13)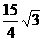 (14)
(14)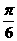
(1)A(2)C(3)C(4)A(5)B(6)A(7)D(8)B(9)B(10)A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com