
题目列表(包括答案和解析)
3.利用计算器,算出自变量和函数值的对应值如下表:
|
x |
0.2 |
0.6 |
1.0 |
1.4 |
1.8 |
2.2 |
2.6 |
3.0 |
3.4 |
… |
|
y=2x |
1.149 |
1.516 |
2.0 |
2.639 |
3.482 |
4.595 |
6.063 |
8.0 |
10.556 |
… |
|
y=x2 |
0.04 |
0.36 |
1.0 |
1.96 |
3.24 |
4.84 |
6.76 |
9.0 |
11.56 |
… |
那么方程2x=x2的一个根所在区间为( )
A.(0.6,1.0) B.(1.4,1.8)
C.(1.8,2.2) D.(2.6,3.0)
[解析] 设f(x)=2x-x2,由表格观察出在x=1.8时,2x>x2,即f(1.8)>0;在x=2.2时,2x<x2,即f(2.2)<0.所以f(1.8)·f(2.2)<0,所以方程2x=x2的一个根位于区间(1.8,2.2)内.故选C.
[答案] C
2.方程2x-1+x=5的解所在的区间是( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,4)
[解析] 令f(x)=2x-1+x-5,则f(2)=2+2-5=-1<0,f(3)=22+3-5=2>0,从而方程在区间(2,3)内有解.故选C.
[答案] C
1.方程x=ln x的根的个数是( )
A.0 B.1
C.2 D.3
[解析] 方法一:令f(x)=ln x-x,
则f(1)=-<0,f(e)=1->0,
∴f(x)在(1,e)内有零点.又f(x)在定义域(0,+∞)上为增函数,
∴f(x)在定义域内仅有1个零点.
方法二:作出y=x与y=ln x的图象观察可知只有一个交点.故选B.
[答案] B
22.是否存在常数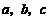 ,使得等式
,使得等式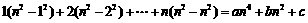 对一切正整数
对一切正整数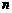 都成立?若存在,求出
都成立?若存在,求出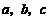 的值;若不存在,说明理由.
的值;若不存在,说明理由.
解:假设存在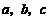 ,使得所给等式成立.
,使得所给等式成立.
令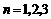 代入等式得
代入等式得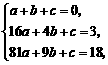 解得
解得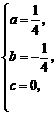
以下用数学归纳法证明等式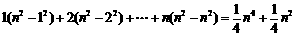 对一切正整数
对一切正整数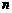 都成立.
都成立.
(1)当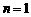 时,由以上可知等式成立;
时,由以上可知等式成立;
(2)假设当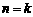 时,等式成立,即
时,等式成立,即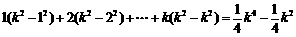 ,
,
则当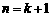 时,
时,
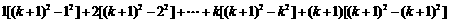
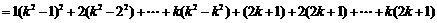
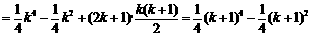 .
.
由(1)(2)知,等式结一切正整数 都成立.
21.由下列不等式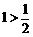 ,
,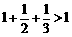 ,
,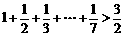 ,
,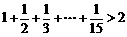 ,
, ,你能得到一个怎样的一般不等式?并加以证明.
,你能得到一个怎样的一般不等式?并加以证明.
解:根据给出的几个不等式可以猜想第 个不等式,即一般不等式为:
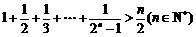 .
.
用数学归纳法证明如下:
(1)当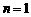 时,
时,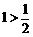 ,猜想成立;
,猜想成立;
(2)假设当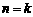 时,猜想成立,即
时,猜想成立,即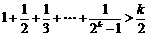 ,
,
则当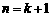 时,
时,
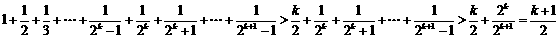 ,即当
,即当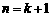 时,
时, 猜想也正确,所以对任意的
猜想也正确,所以对任意的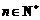 ,不等式成立.
,不等式成立.
20.用三段论方法证明: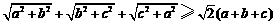 .
.
证明:因为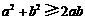 ,所以
,所以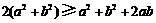 (此处省略了大前提),
(此处省略了大前提),
所以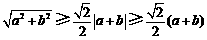 (两次省略了大前提,小前提),
(两次省略了大前提,小前提),
同理,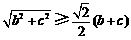 ,
,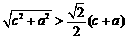 ,
,
三式相加得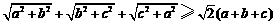 .
.
(省略了大前提,小前提)
19.已知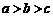 ,且
,且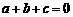 ,求证:
,求证: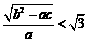 .
.
证明:因为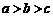 ,且
,且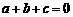 ,
,
所以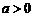 ,
,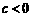 ,要证明原不等式成立,只需证明
,要证明原不等式成立,只需证明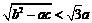 r,
r,
即证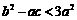 ,从而只需证明
,从而只需证明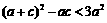 ,
,
即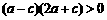 ,
,
因为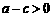 ,
,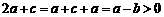 ,
,
所以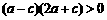 成立,故原不等式成立.
成立,故原不等式成立.
18.已知命题:“若数列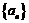 是等比数列,且
是等比数列,且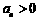 ,则数列
,则数列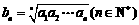 也是等比数列”.类比这一性质,你能得到关于等差数列的一个什么性质?并证明你的结论.
也是等比数列”.类比这一性质,你能得到关于等差数列的一个什么性质?并证明你的结论.
解:类比等比数列的性质,可以得到等差数列的一个性质是:若数列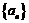 是等差数列,则数列
是等差数列,则数列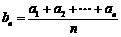 也是等差数列.
也是等差数列.
证明如下:
设等差数列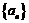 的公差为
的公差为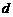 ,则
,则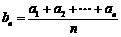
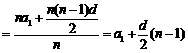 ,
,
所以数列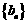 是以
是以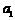 为首项,
为首项,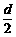 为公差的等差数列.
为公差的等差数列.
17.已知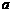 是整
是整 数,
数,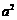 是偶数,求证:
是偶数,求证: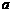 也是偶数.
也是偶数.
证明:(反证法)假设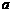 不是偶数,即
不是偶数,即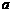 是奇数.
是奇数.
设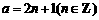 ,则
,则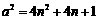 .
.
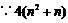 是偶数,
是偶数,
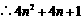 是奇数,这与已知
是奇数,这与已知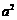 是偶数矛盾.
是偶数矛盾.
由上述矛盾可知,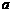 一定是偶数.
一定是偶数.
16.若三角形内切圆的半径为 ,三边长为
,三边长为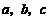 ,则三角形的面积等于
,则三角形的面积等于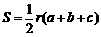 ,根据类比推理的方法,若一个四面体的内切球的半径为
,根据类比推理的方法,若一个四面体的内切球的半径为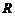 ,四个面的面积分别是
,四个面的面积分别是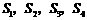 ,则四面体的体积
,则四面体的体积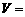 .
.
答案: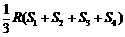
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com