
题目列表(包括答案和解析)
5.5.在证明命题“对于任意角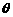 ,
,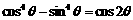 ”的过程:
”的过程:
“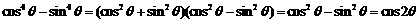 ”中应用了( )
”中应用了( )
A.分析法 B.综合法 C.分析法和综合法综合使用 D.间接证法
答案:B
4.用数学归纳法证明等式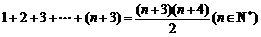 时,第一步验证
时,第一步验证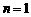 时,左边应取的项是( )
时,左边应取的项是( )
A.1 B.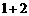 C.
C.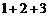 D.
D.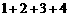
答案:D
3.推理“①正方形是平行四边形;②梯形不是平行四边形;③所以梯形不是正方形”中的小前提是( )
A.① B.② C.③ D.①和②
答案:B
2.图1是一个水平摆放的小正方体木块,图2,图3是由这样的小正方体木块叠放而成的,按照这样的规律放下去,至第七个叠放的图形中,小正方体木块总数就是( )
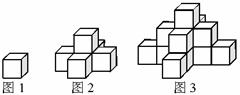
A.25 B.66 C.91 D.120
答案:C
1.下面使用的类比推理中恰当的是( )
A.“若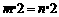 ,则
,则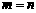 ”类比得出“若
”类比得出“若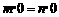 ,则
,则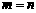 ”
”
B.“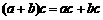 ”类比得出“
”类比得出“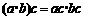 ”
”
C.“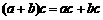 ”类比得出“
”类比得出“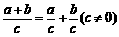 ”
”
D.“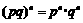 ”类比得出“
”类比得出“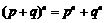 ”
”
答案:C
22.若不等式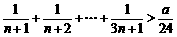 对一切正整数
对一切正整数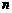 都成立,求正整数
都成立,求正整数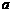 的最大值,并证明结论.
的最大值,并证明结论.
解:当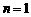 时,
时,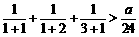 ,即
,即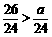 ,
,
所以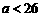 .
.
而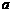 是正整数,所以取
是正整数,所以取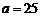 ,下面用数学归纳法证明:
,下面用数学归纳法证明: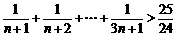 .
.
(1)当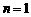 时,已证;
时,已证;
(2)假设当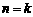 时,不等式成立,即
时,不等式成立,即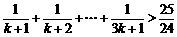 .
.
则当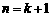 时,
时,
有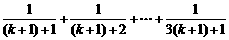
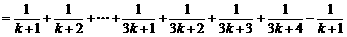
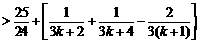 .
.
因为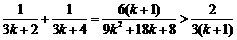 ,
,
所以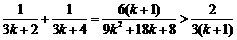 ,
,
所以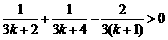 .
.
所以当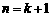 时不等式也成立.
时不等式也成立.
由(1)(2)知,对一切正整数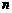 ,都有
,都有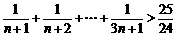 ,
,
所以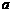 的最大值等于25.
的最大值等于25.
推理与证明综合测试题
21.设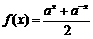 ,
,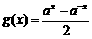 (其中
(其中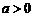 ,且
,且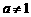 ).
).
(1)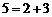 请你推测
请你推测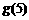 能否用
能否用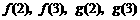 来表示;
来表示;
(2)如果(1)中获得了一个结论,请你推测能否将其推广.
解:(1)由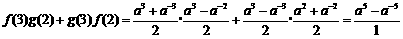 ,
,
又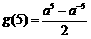 ,
,
因此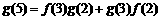 .
.
(2)由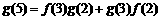 ,即
,即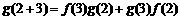 ,
,
于是推测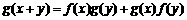 .
.
证明:因为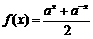 ,
,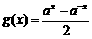 (大前提).
(大前提).
所以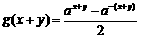 ,
,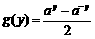 ,
,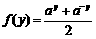 ,(小前提及结论)
,(小前提及结论)
所以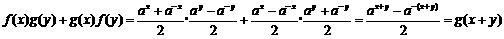 .
.
20.已知实数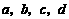 满足
满足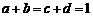 ,
,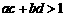 ,求证
,求证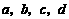 中至少有一个是负数.
中至少有一个是负数.
证明:假设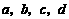 都是非负实数,因为
都是非负实数,因为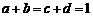 ,
,
所以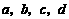
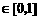 ,所以
,所以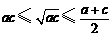 ,
,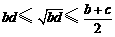 ,
,
所以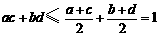 ,
,
这与已知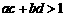 相矛盾,所以原假设不成立,即证得
相矛盾,所以原假设不成立,即证得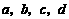 中至少有一个是负数.
中至少有一个是负数.
19.求证:当一个圆和一个正方形的周长相等时,圆的面积比正方形的面积大.
证明:(分析法)设圆和正方形的周长为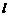 ,依题意,圆的面积为
,依题意,圆的面积为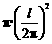 ,正方形的面积为
,正方形的面积为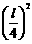 .
.
因此本题只需证明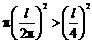 .
.
要证明上式,只需证明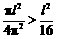 ,
,
两边同乘以正数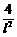 ,得
,得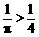 .
.
因此,只需证明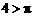 .
.
 上式是成立的,所以
上式是成立的,所以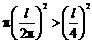 .
.
这就证明了如果一个圆和一个正方形的周长相等,那么圆的面积比正方形的面积最大.
18.如图,已知已知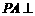 矩形
矩形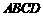 所在平面,
所在平面,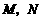 分别是
分别是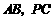 的中点.
的中点.
求证:(1)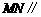 平面
平面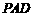 ;(2)
;(2)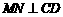 .
.
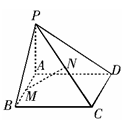 证明:(1)取
证明:(1)取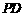 的中点
的中点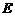 ,连结
,连结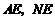 .
.
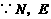 分别为
分别为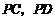 的中点.
的中点.
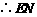 为
为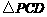 的中位线,
的中位线,
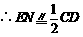 ,
,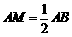 ,而
,而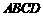 为矩形,
为矩形,
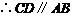 ,且
,且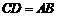 .
.
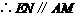 ,且
,且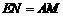 .
.
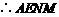 为平行四边形,
为平行四边形,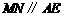 ,而
,而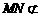 平面
平面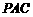 ,
, 平面
平面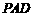 ,
,
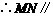 平面
平面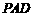 .
.
(2)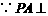 矩形
矩形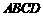 所在平面,
所在平面,
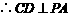 ,而
,而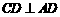 ,
,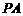 与
与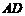 是平面
是平面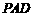 内的两条直交直线,
内的两条直交直线,
 平面
平面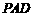 ,而
,而 平面
平面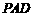 ,
,
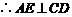 .
.
又 ,
,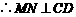 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com