9.已知x轴上的一定点A(1，0)，Q为椭圆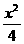+y²=1上的动点，求AQ中点M的轨迹.

8. 椭圆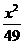 +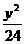=1上有一点P，F₁，F₂分别为椭圆的左、右焦点，且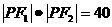，则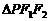的面积为　　　　 。

7.设椭圆的方程为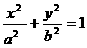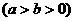，椭圆与Y轴正半轴的一个交点B与两焦点 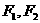组成的三角形的周长为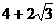，且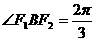，则此椭圆的方程为　　　　 。

6.已知圆C: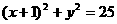及点，Q为圆上一点，AQ的垂直平分线交CQ于M，则M点的轨迹方程为　　　　

5．椭圆的两焦点为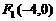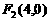，，过F₁作弦AB，且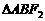的周长为20，则此椭圆的方程为　　　　

4.椭圆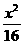 +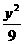=1的左右焦点分别是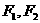，点P在椭圆上，若P,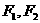是一个直角三角形的三个顶点，则点P到x轴的距离为 [　 ]

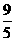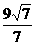A 　　　　　　　　　B 3　　　　　　　　　 C　　　　　　　 D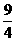

3.椭圆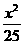 +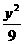=1上一点P到两焦点距离之积为m，则m取最大值时P点坐标为[　 ]

A.(5，0)或(-5，0)　　　 B.(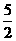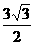，)或(，-)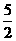

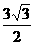C.(0，3)或(0，-3)　　　 D.(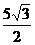,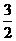)或(-，-)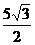

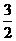2.已知圆O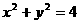：，从这个圆上任意一点P向y轴作垂线段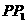(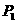在y轴上)，M在直线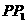上且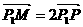，则动点M的轨迹方程是　　　　　　　　　　　　　 [　 ]

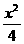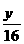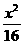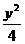A.4x²+16y²=1　 B.16x²+4y²=1　 C.+=1　　 D. +=1

1、椭圆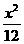 +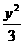=1的焦点为F₁和F₂，点P在椭圆上，如果线段PF₁中点在y轴上，那么|PF₁|是|PF₂|的　　　　　　　　　　　　　　　　　　　　　　　　　　 [　 ]

A.4倍　　　　 B.5倍　　　　 C.7倍　　　　　 D.3倍

20．已知对任意平面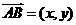向量，把向量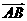绕其起点沿逆时针方向旋转得到向量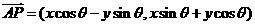，叫做把点B绕点A沿逆时针方向旋转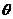角得到点P。

⑴已知平面上点A(1,2)，点B(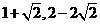)，把点B绕点A沿顺时针方向旋转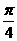角后得到点P，求点P的坐标。

⑵设平面上的曲线C上的每一点绕坐标原点沿逆时针方向旋转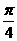角后得到点的轨迹是双曲线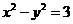，求原来曲线C的方程。

高二数学第一学期期末试卷