
题目列表(包括答案和解析)
4.在直径为10cm的定滑轮上有一条弦,其长为6cm,P是该弦的中点,该滑轮以每秒5弧度的角速度旋转,则点P在5秒内所经过的路程是( )
A.10 cm B.20 cm C.50 cm D.100 cm
3.下列四个关系正确的是( )
A.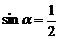 且
且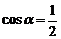 B.
B.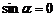 且
且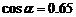
C.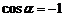 且
且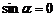 D.
D.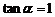 且
且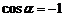
2.若角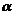 的终边经过点P(2,3),则下列结论正确的是( )
的终边经过点P(2,3),则下列结论正确的是( )
A.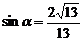 B.
B.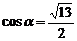 C.
C.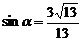 D.
D.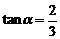
1. 1000º角的终边所在的象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
20、(14分)若对于正整数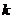 、
、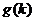 表示
表示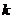 的最大奇数因数,例如
的最大奇数因数,例如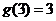 ,
,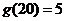 ,
,
并且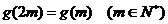 ,设
,设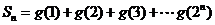
(Ⅰ)求S1、S2、S3 ;
(Ⅱ)求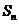 ;
;
(III)设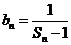 ,求证数列
,求证数列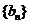 的前
的前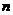 顶和
顶和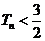 .
.
19、(14分)已知定义在正实数集上的函数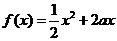 ,
,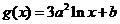 ,其中
,其中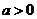 .设两曲线
.设两曲线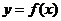 ,
,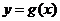 有公共点,且在该点处的切线相同.
有公共点,且在该点处的切线相同.
(I)用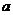 表示
表示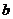 ,并求
,并求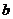 的最大值;
的最大值;
(II)求证: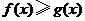 (
(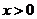 ).
).
18、 (14分)如图,面积为
(14分)如图,面积为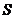 的正方形
的正方形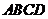 中有一个不规则的图形
中有一个不规则的图形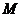 ,可按下面方法估计
,可按下面方法估计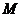 的面积:在正方形
的面积:在正方形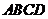 中随机投掷
中随机投掷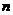 个点,若
个点,若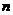 个点中有
个点中有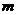 个点落入
个点落入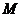 中,则
中,则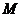 的面积的估计值为
的面积的估计值为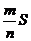 ,假设正方形
,假设正方形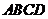 的边长为2,
的边长为2,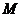 的面积为1,并向正方形
的面积为1,并向正方形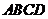 中随机投掷
中随机投掷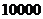 个点,以
个点,以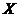 表示落入
表示落入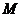 中的点的数目.
中的点的数目.
(I)求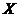 的均值
的均值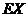 ;
;
(II)求用以上方法估计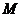 的面积时,
的面积时,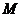 的面积的估计值与实际值之差在区间
的面积的估计值与实际值之差在区间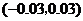 内的概率.
内的概率.
附表: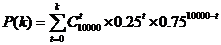
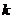
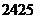
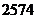
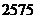
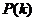
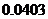
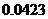
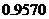
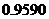
17、(14分)求由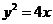 与直线
与直线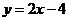 所围成图形的面积.
所围成图形的面积.
16、(12分)已知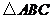 顶点的直角坐标分别为
顶点的直角坐标分别为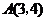 ,
,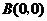 ,
,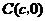 .
.
(1)若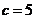 ,求
,求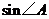 的值;
的值;
(2)若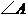 是钝角,求
是钝角,求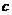 的取值范围.
的取值范围.
15、(12分)在某年一项关于16艘轮船的研究中,船的吨位区间从192吨到3246吨,船员的数目从5人到32人.船员人数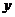 关于船的吨位
关于船的吨位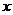 的线性回归方程为
的线性回归方程为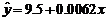
(1)假设两艘轮船吨位相差1000吨,则船员平均人数相差多少?
(2)对于最小的船估计的船员数是多少?对于最大的船估计的船员数是多少?(保留整数)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com