
题目列表(包括答案和解析)
2、边长为a的正方形ABCD沿对角线BD折叠成直二面角后,AC的长为 ( )
A 、 a
B 、 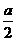 C
、
C
、 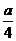 D
、
D
、 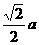
1、若平面α、β互相垂直,则 ( )
A、α中的任意一条直线垂直于β B、α中有且只有一条直线垂直于β
C、平行于α的直线垂直于β D、α内垂直于交线的直线必垂直于β
3、 已知⊿ABC,AC=BC=1,AB=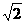 ,又知⊿ABC所在平面外一点S,SA=SB=2,SC=
,又知⊿ABC所在平面外一点S,SA=SB=2,SC=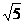 ,点P是SC的中点,求:
,点P是SC的中点,求:
⑴ 二面角S-AC-B的大小
⑵ 点P到平面ABC的距离
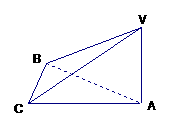 1、如图,在立体图形V-ABC中,∠VAB=∠VAC=∠ABC=900,平面VAB和平面VBC有何种位置关系?请说明理由
1、如图,在立体图形V-ABC中,∠VAB=∠VAC=∠ABC=900,平面VAB和平面VBC有何种位置关系?请说明理由
2、 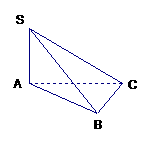 如图,四面体SABC中,⊿ABC是等腰三角形,AB=BC=2a,∠ABC=
如图,四面体SABC中,⊿ABC是等腰三角形,AB=BC=2a,∠ABC=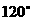 ,且SA⊥平面ABC,SA=3a,求点A到平面SBC的距离
,且SA⊥平面ABC,SA=3a,求点A到平面SBC的距离
2、已知平面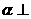 平面
平面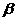 ,直线
,直线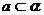 ,
,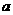 与
与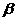 不垂直,则
( )
不垂直,则
( )
A、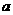 垂直于
垂直于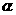 与
与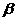 的交线
B、
的交线
B、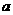 不垂直于
不垂直于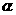 与
与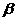 的交线
的交线
C、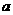 可能垂直于
可能垂直于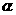 与
与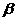 的交线也可能不垂直于
的交线也可能不垂直于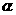 与
与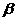 的交线
D、以上都不对
的交线
D、以上都不对
1、 已知两个平面互相垂直,那么下列命题中正确命题的个数是 ( )
①一个平面内的直线必垂直于另一个平面内的无数条直线 ②一个平面内且垂直于这两个平面交线的直线必垂直于另一个平面内的任意一条直线 ③一个平面内的任何一条直线必垂直于另一个平面 ④过一个平面内的任意一点作交线的垂线,则此直线必垂直于另一个平面
A、 4 B、3 C、2 D、1
2、过正方形ABCD的顶点A作PA⊥平面ABCD,设PA=AB=a,求二面角B-PC-D的大小
1、P为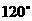 的二面角
的二面角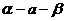 内一点,P到
内一点,P到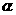 和
和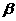 的距离均为10,求P到棱
的距离均为10,求P到棱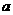 的距离
的距离
2、河堤斜面与水平面所成的二面角为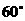 ,堤面上有一条直道CD,它与坡脚的水平线的夹角为300,沿这条直道从坡脚向上行走
,堤面上有一条直道CD,它与坡脚的水平线的夹角为300,沿这条直道从坡脚向上行走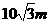 时人升高了
米
时人升高了
米
1、在300的二面角的一个面内有一个点,若它到另一个面的距离是10,则它到棱的距离为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com