
题目列表(包括答案和解析)
21. (本小题满分16分)
已知椭圆C: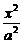 +
+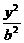 =1(a>b>0),两个焦点分别为F1和F2,斜率为k的直线l过右焦点F2且与椭圆交于A.B两点,设l与y轴交点为P,线段PF2的中点恰为B。
=1(a>b>0),两个焦点分别为F1和F2,斜率为k的直线l过右焦点F2且与椭圆交于A.B两点,设l与y轴交点为P,线段PF2的中点恰为B。
(1)若|k|≤ ,求椭圆C的离心率的取值范围;
,求椭圆C的离心率的取值范围;
(2)若k= ,A.B到右准线距离之和为
,A.B到右准线距离之和为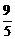 ,求椭圆C的方程。
,求椭圆C的方程。
解:(1)设右焦点F2(c,0),则l:y=k(x-c).令x=0,则y=-ck,∴P(0,-ck)。
∵B为F2P的中点,∴B(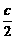 ,-
,-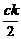 )。
)。
∵B在椭圆上,∴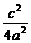 +
+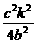 =1。
=1。
∴k2=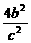 ·
·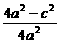 =(
=(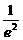 -1)(4-e2)=
-1)(4-e2)=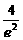 +e2-5。
+e2-5。
∵|k|≤ ,∴
,∴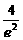 +e2-5≤
+e2-5≤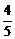 .∴(5e2-4)(e2-5)≤0。∴
.∴(5e2-4)(e2-5)≤0。∴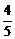 ≤e2<1.∴
≤e2<1.∴ ≤e<1.
≤e<1.
(2)k= ,∴e=
,∴e= .∴
.∴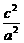 =
=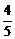 .
.
∴a2=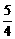 c2,b2=
c2,b2=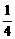 c2.椭圆方程为
c2.椭圆方程为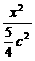 +
+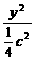 =1,即x2+5y2=
=1,即x2+5y2=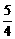 c2.
c2.
直线l方程为y= (x-c),
(x-c),
B(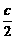 ,-
,-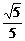 c),右准线为x=
c),右准线为x=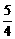 c.
c.
设A(x0,y0),则(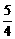 c-x0)+(
c-x0)+(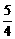 c-
c-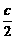 )=
)=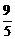 ,∴x0=2c-
,∴x0=2c-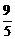 ,y0=
,y0= (c-
(c-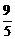 ).
).
∵A在椭圆上,∴(2c-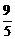 )2+5[
)2+5[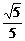 (c-
(c-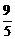 )]2=
)]2=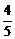 c2.
c2.
解之得c=2或c=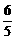 (不合题意,舍去).
(不合题意,舍去).
∴椭圆方程为x2+5y2=5,即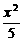 +y2=1.
+y2=1.
第III卷(理科附加题)
(第1、2、3、4题每题6分,第5题16分 共40分)
20. (本小题满分16分)
如图所示,已知A、B、C是长轴长为4的椭圆上的三点,点A是长轴的一个端点,BC过椭圆中心O,且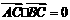 ,BC=2AC.
,BC=2AC.
(I)建立适当的坐标系,求椭圆方程;
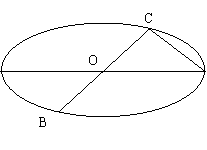 (II)如果椭圆上有两点P、Q,使∠PCQ的平分线垂直于AO,证明:存在实数λ,使
(II)如果椭圆上有两点P、Q,使∠PCQ的平分线垂直于AO,证明:存在实数λ,使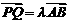 .
.
解:(I)以O为原点,OA为X轴建立直角坐标系,设A(2,0),则椭圆方程为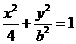
∵O为椭圆中心,∴由对称性知|OC|=|OB|
|
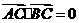 , ∴AC⊥BC
, ∴AC⊥BC
又∵|BC|=2|AC| ∴|OC|=|AC|
∴△AOC为等腰直角三角形
∴点C的坐标为(1,1) ∴点B的坐标为(-1,-1)
将C的坐标(1,1)代入椭圆方程得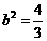 ,
,
则求得椭圆方程为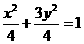
(II)由于∠PCQ的平分线垂直于OA(即垂直于x轴),不妨设PC的斜率为k,则QC的斜率为-k,因此PC、QC的直线方程分别为y=k(x-1)+1,y=-k(x-1)+1
由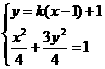 得(1+3k2)x2-6k(k-1)x+3k2-6k-1=0 *)
得(1+3k2)x2-6k(k-1)x+3k2-6k-1=0 *)
∵点C(1,1)在椭圆上,
∴x=1是方程(*)的一个根,∴xP•1=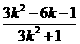 即xP=
即xP=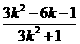
同理xQ=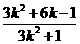
∴直线PQ的斜率为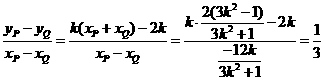 (定值)
(定值)
又∠ACB的平分线也垂直于OA
∴直线PQ与AB的斜率相等(∵kAB=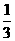 )
)
∴向量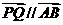 ,即总存在实数
,即总存在实数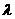 ,使
,使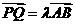 成立.
成立.
19.解:⑴以C为原点,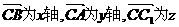 轴建立空间直角坐标系.
轴建立空间直角坐标系.
设AC=2,则C(0,0,0),A(0,2,0),C1(0,0,2)E(1,1,0)
设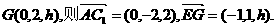
由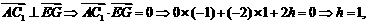 即点
即点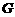 为
为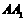 的中点。
的中点。
⑵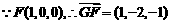 .
. 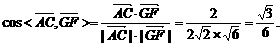
19.(本小题满分14分)用向量法求解下列问题
如图,在直三棱柱ABC-A1B1C1中,AC=BC=AA1,∠ACB=90°,E、F分别是AB、BC的中点,G是AA1上的点.
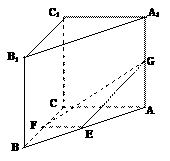 ⑴如果
⑴如果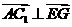 ,试确定点G的位置;
,试确定点G的位置;
⑵在满足条件(Ⅰ)的情况下,试求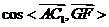 的值。
的值。
19.(本小题满分14分)
求下列函数的导数:
(1)y=x2sinx; (2)
y=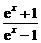 ;
;
解:(1)y′=(x2)′sinx+x2(sinx)′=2xsinx+x2cosx.
(2)y′=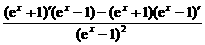 =
=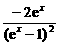 .
.
18.(本小题满分14分)
已知抛物线C:y2=4x动直线L:y=k(x+1)与抛物线C交于A、B两点,O为原点
①求证: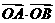 定值;
定值;
②求满足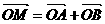 的点M的轨迹方程。
的点M的轨迹方程。
17.(本小题满分14分)
已知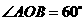 ,
,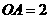 ,
,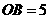 ,根据下列条件求
,根据下列条件求 为钝角三角形的概率:
为钝角三角形的概率:
⑴在线段OB上任取一点C;
⑵过点A任作一直线与直线OB交于点C。
解:(1)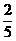 ;
(2)
;
(2)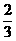 .
.
16. 为了科学地比较考试的成绩,有些选拔性考试常常将考试分数转化为标准分,转化关系式为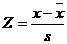 (其中
(其中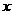 是某位学生的考试分数,
是某位学生的考试分数, 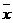 是该次考试的平均分,s是该次考试的标准差,Z称为这位学生的标准分),转化成标准分后可能出现小数或负数,因此,又常常再将Z分数作线性变换转化成其他分数。例如某次学业选拔考试采用的是T分数,线性变换公式是:
是该次考试的平均分,s是该次考试的标准差,Z称为这位学生的标准分),转化成标准分后可能出现小数或负数,因此,又常常再将Z分数作线性变换转化成其他分数。例如某次学业选拔考试采用的是T分数,线性变换公式是: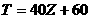 ,已知在这次考试中某位考生的考试分数是85,这次考试的平均分是70,标准差是25,则该考生的T分数为_______84_____.
,已知在这次考试中某位考生的考试分数是85,这次考试的平均分是70,标准差是25,则该考生的T分数为_______84_____.
15.若双曲线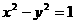 的右支上一点P(a,b)直线y=x的距离为
的右支上一点P(a,b)直线y=x的距离为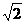 ,则a+b 的值是
,则a+b 的值是 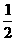
14.已知实数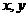 满足
满足 ,则
,则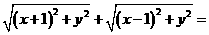 4 。
4 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com