
题目列表(包括答案和解析)
5、已知函数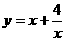 (x>0),则函数的最小值为是( )
(x>0),则函数的最小值为是( )
A.-4 B.2 C.4 D.无
4、不等式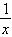 < 2的解集是:( )
< 2的解集是:( )
A、{x|x>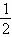 } B、{x|x<0} C、{x|x<0或x>
} B、{x|x<0} C、{x|x<0或x>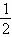 } D、{x|0<x<
} D、{x|0<x<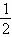 }
}
3、若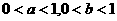 ,则
,则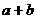 ,
,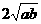 ,
,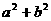 ,
,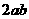 中最大一个是( )
中最大一个是( )
A.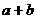 B.
B.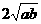 C.
C.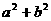 D.
D.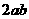
2、直线2x-y+1=0与直线x+2y-5=0的位置关系是:( )
A、平行 B、重合 C、垂直 D、相交但不垂直
1、直线y=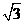 x+1的倾斜角为
( )
x+1的倾斜角为
( )
A. 150º
B. 60º C.120º D. 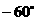
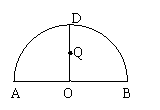
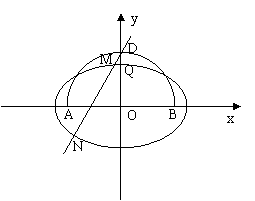
5.如图,ADB为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知AB=4,曲线C过Q点,动点P在曲线C上运动,且保持PA+PB的值不变。
(1)建立适当的坐标系,求曲线C的方程。
(2)过D点的直线L与曲线C相交于不同的两点M,N,求△OMN面积的最大值。
 (3)若过D的直线L与曲线C相交于不同两点M,N,且M在D,N之间,设
(3)若过D的直线L与曲线C相交于不同两点M,N,且M在D,N之间,设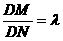 ,求λ的取值范围.
,求λ的取值范围.
解:以AB、OD所在直线分别为x轴,y轴,O为原点,建立直角坐标系,∵ïAB÷ =4 ∴A(-2,0) B(2,0),D(0,2) ∴ïPAï+ïPBï=ïQAï+ïQBï=2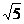 >ïAB÷ =4
>ïAB÷ =4
∴曲线C为以O为中心,A,B为焦点的椭圆,设其长半轴为a,短半轴为b,半焦距为c,
则2a=2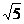 ,2c=4, ∴a=
,2c=4, ∴a=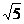 , c=2 , b=1 ∴曲线C方程为
, c=2 , b=1 ∴曲线C方程为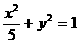
 (2)设直线L的方程为y=kx+2,代入曲线C的方程得(1+5k2)x2+20kx+15=0,设M(x1,y1),N(x2,y2)
(2)设直线L的方程为y=kx+2,代入曲线C的方程得(1+5k2)x2+20kx+15=0,设M(x1,y1),N(x2,y2)
 则 △=(20k)2-4(1+5k2) ·15>0 ①
则 △=(20k)2-4(1+5k2) ·15>0 ①
x1 + x2 =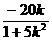
x1 ·x2 =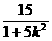
由①得k2>3/5
点O到直线MN的距离d=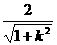
弦MN的长ïMNï=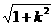 ïx1 - x2ï=
ïx1 - x2ï=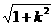
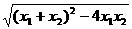 =
=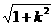
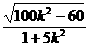
∴S△OMN =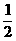 ïMNï·d=
ïMNï·d=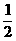
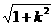 ·
·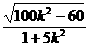 ·
·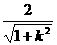 =
=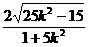
设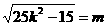 ∵k2
=
∵k2
=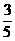 ∴m>0
∴m>0
则k2 =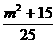 ∴S△OMN=
∴S△OMN=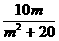 ≤
≤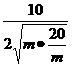 =
=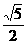
当且仅当m=20/m即m=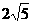 时等号成立,此时k2=
时等号成立,此时k2=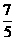 ∴△OMN的最大面积为
∴△OMN的最大面积为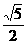
(3)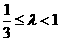
思路点拨:由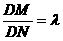 得
得
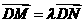 ,从而得到M、N的坐标与D点坐标之间的关系:
,从而得到M、N的坐标与D点坐标之间的关系:
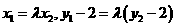 ,代入到椭圆
,代入到椭圆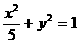 方程中,将可以消去
方程中,将可以消去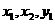 ,得到
,得到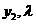
的关系,利用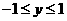 及
及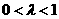 ,即得。
,即得。
4.过双曲线x2-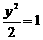 的右焦点作直线交双曲线于A、B两点,且
的右焦点作直线交双曲线于A、B两点,且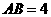 ,则这样的直线有
,则这样的直线有
3 条。
3.已知实数x,y满足3x2+2y2=6x,则x2+y2的最大值是 4 。
2.双曲线x2-y2=1的左焦点为F,点P为左支下半支上任意一点(异于顶点),则直线PF的斜率的变化范围是
A.(-∞,0) B.(1,+∞)
C.(-∞,0)∪(1,+∞) D.(-∞,-1)∪(1,+∞)
解析:数形结合法,与渐近线斜率比较。答案:C
1.在直角坐标系中,方程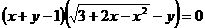 所表示的曲线为( D )
所表示的曲线为( D )
A.一条直线和一个圆 B.一条线段和一个圆
C.一条直线和半个圆 D.一条线段和半个圆
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com