
题目列表(包括答案和解析)
20.(本小题满分16分)
已知函数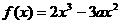 ,
,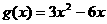 ,又函数
,又函数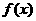 在
在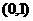 单调递减,而在
单调递减,而在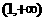 单调递增.
单调递增.
(1)求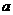 的值;
的值;
(2)求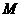 的最小值,使对
的最小值,使对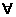
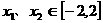 ,有
,有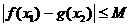 成立;
成立;
(3)是否存在正实数 ,使得
,使得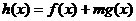 在
在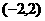 上既有最大值又有最小值?若存在,求出m的取值范围;若不存在,请说明理由.
上既有最大值又有最小值?若存在,求出m的取值范围;若不存在,请说明理由.
19.(本小题满分16分)
椭圆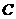 :
: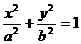
 的一个焦点
的一个焦点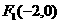 ,右准线方程
,右准线方程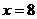 .
.
(1)求椭圆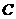 的方程;
的方程;
(2)若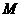 为右准线上一点,
为右准线上一点, 为椭圆
为椭圆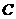 的左顶点,连结
的左顶点,连结 交椭圆于点
交椭圆于点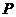 ,求
,求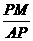 的取值范围;
的取值范围;
(3)圆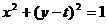 上任一点为
上任一点为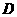 ,曲线
,曲线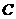 上任一点为
上任一点为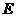 ,如果线段
,如果线段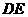 长的最大值为
长的最大值为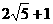 ,求
,求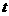 的值.
的值.
18.(历史方向考生做)(本小题满分15分)
在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(1)根据以上数据建立一个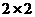 的列联表;
的列联表;
(2)试判断性别与休闲方式是否有关系(可靠性不低于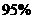 ).
).
附:(1)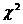 的计算公式:
的计算公式: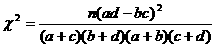 ;
;
(2)临值表:
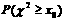 |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
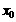 |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
18.(物理方向考生做)(本小题满分15分)
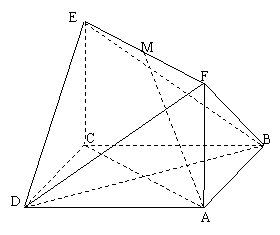
如图,已知正方形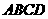 和
和
矩形 所在平面互相垂直,
所在平面互相垂直,
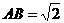 ,
,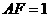 ,
,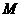 是线段
是线段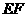 的中点.
的中点.
(1)求证:AM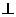 平面BDF;
平面BDF;
(2)求二面角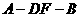 的大小;
的大小;
(3)试在线段 上确定一点
上确定一点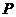 ,使
,使
得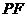 与
与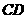 所成的角是
所成的角是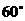 .
.
17.(本小题满分15分)
设关于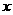 的一元二次方程
的一元二次方程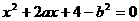 .
.
(1)如果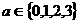 ,
,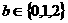 ,求方程有实根的概率;
,求方程有实根的概率;
(2)如果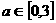 ,
,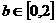 ,求方程有实根的概率;
,求方程有实根的概率;
 (3)由(2),并结合课本“撒豆子”试验,请你设计一个估算圆周率
(3)由(2),并结合课本“撒豆子”试验,请你设计一个估算圆周率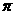 的实验,并给出计算公式.
的实验,并给出计算公式.
16.(本小题满分14分)
设命题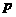 :曲线
:曲线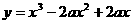 上任一点处的切线的倾斜角都是锐角;命题
上任一点处的切线的倾斜角都是锐角;命题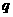 :直线
:直线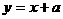 与曲线
与曲线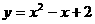 有两个公共点;若命题
有两个公共点;若命题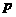 和命题
和命题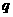 中有且只有一个是真命题,求实数
中有且只有一个是真命题,求实数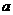 的取值范围.
的取值范围.
15.(本小题满分14分)
为了了解某中学高二女生的身高情况,该校对高二女生的身高进行了一次随机抽样测量,所得数据整理后列出了频率分布表如下:(单位: )
)
|
分 组 |
频数 |
频率 |
|
[150.5,154.5) |
1 |
0.02 |
|
[154.5,158.5) |
4 |
0.08 |
|
[158.5,162.5) |
20 |
0.40 |
|
[162.5,166.5) |
15 |
0.30 |
|
[166.5,170.5) |
8 |
0.16 |
|
[170.5,174.5] |
m |
n |
|
合计 |
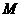 |
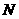 |

(1)表中 、
、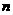 、
、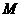 、
、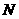 所表示的数分别是多少?
所表示的数分别是多少?
(2)绘制频率分布直方图;
(3)估计该校女生身高小于162.5 的百分比.
的百分比.
14.给出下列命题:
①若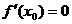 ,则函数
,则函数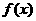 在
在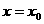 处有极值;
处有极值;
②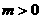 是方程
是方程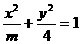 表示椭圆的充要条件;
表示椭圆的充要条件;
③若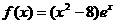 ,则
,则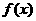 的单调递减区间为
的单调递减区间为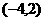 ;
;
④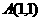 是椭圆
是椭圆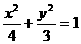 内一定点,
内一定点,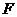 是椭圆的右焦点,则椭圆上存在点
是椭圆的右焦点,则椭圆上存在点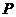 ,使得
,使得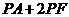 的最小值为3.
的最小值为3.
其中为真命题的序号是 ▲ .
13.(物理方向考生做)函数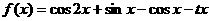 在
在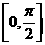 上单调递增,则实数
上单调递增,则实数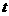 的取值范围是 ▲ .
的取值范围是 ▲ .
(历史方向考生做)函数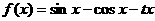 在
在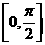 上单调递增,则实数
上单调递增,则实数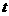 的取值范围是 ▲ .
的取值范围是 ▲ .
12.将一颗骰子先后抛掷两次,观察向上的点数,则两次观察到的点数之和为数字 ▲ 的概率是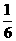 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com