
题目列表(包括答案和解析)
7、已知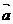 、
、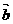 为任意非零向量,有下列命题:
为任意非零向量,有下列命题:
(1)|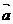 |=|
|=|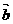 |;(2)(
|;(2)(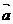 )2=(
)2=(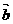 )2;(3)(
)2;(3)(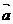 )2=
)2=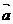 ·
·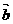
其中可以作为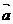 =
=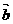 的必要且非充分条件的命题是( )。
的必要且非充分条件的命题是( )。
A.(1) B.(1)(2) C.(2)(3) D.(1)(2)(3)
6、已知A(1,0,0), B(0,-1,1),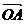 +
+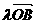 与
与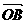 的夹角为120°,则
的夹角为120°,则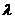 的值为( )。
的值为( )。
A.±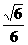 B.
B.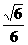 C.-
C.-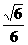 D.±
D.±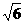
5、正方体ABCD-A1B1C1D1中,二面角A1-BC1-D1的正切值为( )。
A.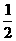 B.
B.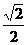 C.1
D.
C.1
D.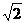
4、△ABC中,角A、B的对边分别是a、b,且A=2B,则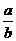 的取值范围是( )。
的取值范围是( )。
A.(1,2) B.(0,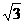 ) C.(
) C.(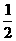 ,1) D.(0,2)
,1) D.(0,2)
3、椭圆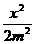 +
+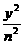 =1与双曲线
=1与双曲线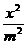 -
-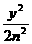 =1有共同的焦点,则椭圆的离心率为( )。
=1有共同的焦点,则椭圆的离心率为( )。
A.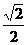 B.
B.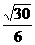 C.
C.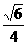 D.
D.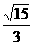
2、设等比数列{an}的前n项和为Sn,若a2008=2S2007+6, a2009=2S2008+6, 则数列{an}的公比q为( )。
A.2 B.4 C.5 D.3
1、设原命题:若a+b≥2,则a、b中至少有一个不小于1,原命题与其逆命题的真假情况是( )。
A.原命题真,逆命题假 B.原命题假,逆命题真
C.原命题与逆命题均为真命题 D.原命题与逆命题均为假命题
20.证明:(1)由PA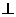 平面ABCD
平面ABCD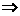
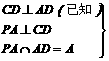
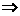
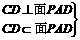
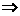 平面PDC
平面PDC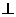 平面PAD;
平面PAD;
(2)取PD中点为F,连结EF、AF,由E为PC中点,
得EF为△PDC的中位线,则EF//CD,CD=2EF.
又CD=2AB,则EF=AB.由AB//CD,则EF∥AB.
所以四边形ABEF为平行四边形,则EF//AF.
由AF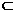 面PAD,则EF//面PAD.
面PAD,则EF//面PAD.
19.(1)∵O、D分别为AC、PC的中点,∴OD∥PA. 又PA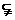 平面PAB,∴OD∥平面PAB.
平面PAB,∴OD∥平面PAB.
(2)∵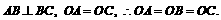 又∵
又∵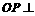 平面ABC,∴PA=PB=PC,
平面ABC,∴PA=PB=PC,
取BC中点E,连结PE和OE,则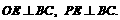 ∴
∴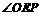 是所求二面角的平面角.
是所求二面角的平面角.
又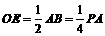 ,易求得
,易求得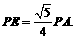 在直角
在直角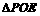 中,
中,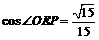 ,
,
∴二面角A-BC-P的大小为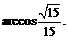
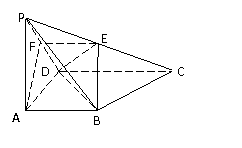
20. 如图,四棱锥P-ABCD中, PA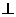 平面ABCD,底面ABCD是直角梯形,AB⊥AD,CD⊥AD,CD=2AB,E为PC中点.
平面ABCD,底面ABCD是直角梯形,AB⊥AD,CD⊥AD,CD=2AB,E为PC中点.
(I) 求证:平面PDC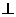 平面PAD;
平面PAD;
(II) 求证:BE//平面PAD.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com