
题目列表(包括答案和解析)
6.函数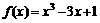 在闭区间[-3,0]上的最大值、最小值分别是 ( )
在闭区间[-3,0]上的最大值、最小值分别是 ( )
A. 1,-17 B.3,-17 C.1,-1 D.9,-19
5. 方程
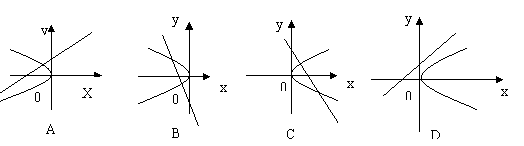
方程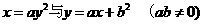 的图像只可能是下图中 ( )
的图像只可能是下图中 ( )
4.过点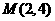 作直线
作直线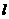 ,与抛物线
,与抛物线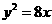 只有一个公共点,满足条件的直线有( )条
只有一个公共点,满足条件的直线有( )条
A.0条 B.1条 C.2条 D.条
3.已知椭圆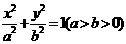 的两准线间的距离为
的两准线间的距离为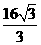 ,离心率为
,离心率为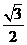 ,则椭圆方程为( )
,则椭圆方程为( )
A.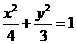 B.
B.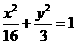 C.
C.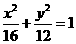 D.
D.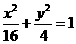
2.设k>1,则关于x、y的方程(1-k)x2+y2=k2-1所表示的曲线是 ( )
A.长轴在y轴上的椭圆 B.长轴在x轴上的椭圆
C.实轴在y轴上的双曲线 D.实轴在x轴上的双曲线
1.已知物体运动的方程是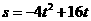 (
(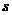 的单位:
的单位: ;
; 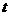 的单位:
的单位: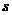 ),则该物体在
),则该物体在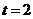
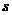 时的速度为( )
时的速度为( )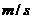 。 ( )
。 ( )
A. 0 B. 1 C. 2 D. 3
17已知圆x2+y2=1,直线y=x+m. (1)m为何值时,直线与圆有两个不同的交点?
(2)设直线与圆交于A,B,且直线OA,OB(O为坐标原点)与x轴的正半轴所成的角为α,β,求证:sin(α+β)是与m无关的定值.
17解(1)直线的方程代入圆的方程,可得2x2+2mx+m2-1=0,由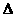 >1,可得4m2-8(m2-1)>0
>1,可得4m2-8(m2-1)>0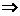 -
-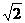 <m<
<m<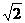 .
.
(2)设A(x1,y1),B(x2,y2),则sinα=y1,cosα=x1,sinβ=y2,cosβ=x2,又y1=x1+m,y2=x2+m,2x2+2mx+m2-1=0,所以x1+x2=-m,x1·x2=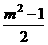 .
.
所以,sin(α+β)=x2y1+x1y2=2x1x2+m(x1+x2)=m2-1+m(-m)=-1(定值).
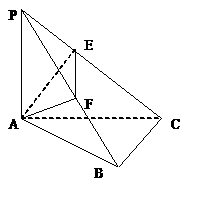 18在空间四边形PABC中,PA
18在空间四边形PABC中,PA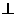 面ABC,AC
面ABC,AC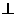 BC,若A在PB,PC上的射影分别是E,F.求证:EF
BC,若A在PB,PC上的射影分别是E,F.求证:EF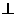 PB
PB
18证明: PA
PA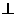 面ABC
面ABC  PA
PA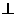 BC--1分,又
BC--1分,又 AC
AC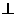 BC,PA
BC,PA AC=A,
AC=A,  BC
BC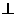 面PAC-----4分,
面PAC-----4分, AF
AF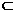 面PAC,
面PAC,  BC
BC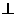 AF-------5分,又
AF-------5分,又 F是点A在PC上的射影,
F是点A在PC上的射影, AF
AF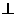 PC--6分,
PC--6分, AF
AF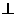 面PBC------8分,
面PBC------8分, AE在平面PBC上的射影为EF-----9分,
AE在平面PBC上的射影为EF-----9分, E是A点在PB上的射影--10分,
E是A点在PB上的射影--10分, AE
AE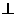 PB
PB  EF
EF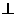 PB----12分
PB----12分
19已知椭圆的中心在原点,焦点在x轴上,一条准线的方程为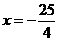 ,焦点到相应准线的距离为
,焦点到相应准线的距离为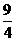 . (1)求该椭圆的标准方程;(2)写出该椭圆的长轴长,短轴长,离心率,焦点坐标和顶点坐标; (3)求以已知椭圆的焦点为顶点,而以椭圆的顶点为焦点的双曲线方程.
. (1)求该椭圆的标准方程;(2)写出该椭圆的长轴长,短轴长,离心率,焦点坐标和顶点坐标; (3)求以已知椭圆的焦点为顶点,而以椭圆的顶点为焦点的双曲线方程.
19解:(1)设椭圆的标准方程是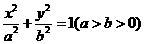 ,则
,则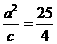 ……①,
……①,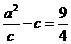 ……②联立①②解得
……②联立①②解得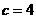 ,
,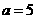 ,所以
,所以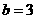 ,故所求的椭圆方程为
,故所求的椭圆方程为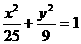 .
.
(2)椭圆的长轴长为10,短轴长为6,离心率为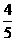 ,焦点坐标为(-4,0),(4,0),顶点坐标为(-5,0),(5,0),(0,-3),(0,3).
,焦点坐标为(-4,0),(4,0),顶点坐标为(-5,0),(5,0),(0,-3),(0,3).
(3)可设双曲线的方程为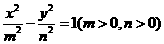 ,由于以已知椭圆的焦点为顶点,而以椭圆的顶点为焦点,故
,由于以已知椭圆的焦点为顶点,而以椭圆的顶点为焦点,故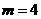 且
且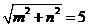 ,所以
,所以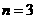 .所求双曲线方程是
.所求双曲线方程是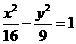 .
.
20已知抛物线的顶点在原点,它的准线经过双曲线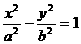 的左焦点,且与x轴垂直,抛物线与此双曲线交于点(
的左焦点,且与x轴垂直,抛物线与此双曲线交于点(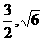 ),求抛物线与双曲线的方程.
),求抛物线与双曲线的方程.
20解:由题意可知抛物线的焦点到准线间的距离为2C(即双曲线的焦距).设抛物线的方程为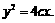 4分
4分
∵抛物线过点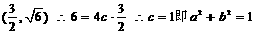 ①
①
又知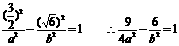 ② 8分
② 8分
由①②可得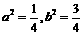 , 10分
, 10分
∴所求抛物线的方程为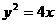 ,双曲线的方程为
,双曲线的方程为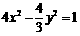 .··· 12分
.··· 12分
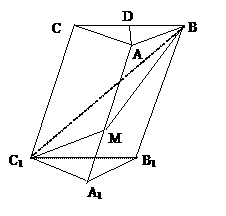 21在斜三棱柱A1B1C1-ABC中, 底面是等腰三角形
21在斜三棱柱A1B1C1-ABC中, 底面是等腰三角形
, AB=AC, 侧面BB1C1C⊥底面ABC.
(Ⅰ)若D是BC的中点, 求证:AD⊥CC1;
(Ⅱ)过侧面BB1C1C的对角线BC1的平面交侧棱
于M, 若AM=MA1, 求证:截面MBC1⊥侧面BB1C1C;
(Ⅲ) AM=MA1是截面MBC1⊥平面BB1C1C的充要
条件吗? 请你叙述判断理由.
21 (Ⅰ)证明: ∵AB=AC, D是BC的中点, ∴AD⊥BC. ∵底面ABC⊥平面BB1C1C, ∴AD⊥侧面BB1C1C. ∴AD⊥CC1.
(Ⅱ)延长B1A1与BM交于N, 连结C1N. ∵AM=MA1, ∴NA1=A1B1. ∵A1B1=A1C1, ∴A1C1= A1N=A1B1. ∴C1N⊥C1B1. ∵截面N B1C1⊥侧面BB1C1C,
∴C1N⊥侧面BB1C1C. ∴截面C1N B⊥侧面BB1C1C. ∴截面MBC1⊥侧面BB1C1C.
(Ⅲ)解: 结论是肯定的, 充分性已由(2)证明,
下面证必要性: 过M作ME⊥B
C1于E, ∵截面MBC1⊥侧面BB1C1C, ∴ME⊥侧面BB1C1C. 又∵AD⊥侧面BB1C1C, ∴ME∥AD. ∴M,
E, A, D共线. ∵A
M∥侧面BB1C1C,
∴AM∥DE.
∵CC1⊥AM, ∴DE∥CC1. ∵D是BC的中点, ∴E是BC1的中点.
∴AM= DE=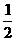 CC1=
CC1=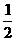 AA1. ∴AM=
MA1.
AA1. ∴AM=
MA1.
22 (理)已知双曲线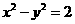 的右焦点为
的右焦点为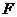 ,过点
,过点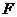 的动直线与双曲线相交于
的动直线与双曲线相交于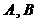 两点,点
两点,点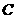 的坐标是
的坐标是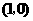 .
.
(I)证明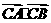 为常数;
为常数;
(II)若动点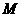 满足
满足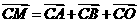 (其中
(其中 为坐标原点),求点
为坐标原点),求点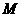 的轨迹方程.
的轨迹方程.
[解析]由条件知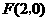 ,设
,设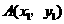 ,
,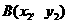 .
.
(I)当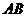 与
与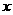 轴垂直时,可设点
轴垂直时,可设点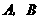 的坐标分别为
的坐标分别为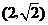 ,
,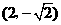 ,
,
此时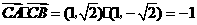 .
.
当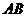 不与
不与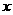 轴垂直时,设直线
轴垂直时,设直线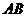 的方程是
的方程是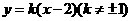 .代入
.代入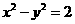 ,有
,有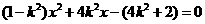 .则
.则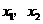 是上述方程的两个实根,所以
是上述方程的两个实根,所以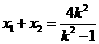 ,
,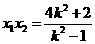 ,于是
,于是
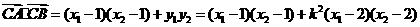
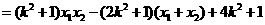
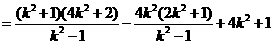
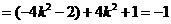 .
.
综上所述,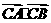 为常数
为常数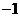 .
.
(II)解法一:设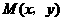 ,则
,则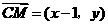 ,
,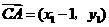 ,
,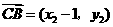 ,
,
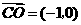 ,由
,由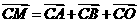 得:
得: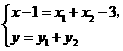 即
即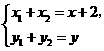
于是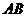 的中点坐标为
的中点坐标为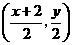 .
.
当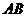 不与
不与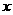 轴垂直时,
轴垂直时,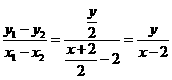 ,即
,即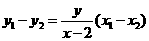 .
.
又因为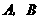 两点在双曲线上,所以
两点在双曲线上,所以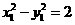 ,
,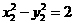 ,两式相减得
,两式相减得
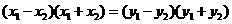
即:
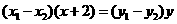 .
.
将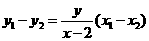 代入上式,化简得
代入上式,化简得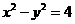 .
.
当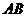 与
与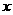 轴垂直时,
轴垂直时,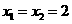 ,求得
,求得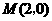 ,也满足上述方程.
,也满足上述方程.
所以点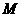 的轨迹方程是
的轨迹方程是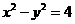 .
.
解法二:同解法一得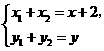 ……………………………………①
……………………………………①
当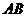 不与
不与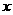 轴垂直时,由(I) 有
轴垂直时,由(I) 有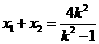 .…………………②
.…………………②
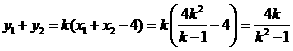 . ………………………………③
. ………………………………③
由①②③得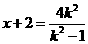 . …………………………………………………④
. …………………………………………………④
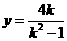 .……………………………………………………………………⑤
.……………………………………………………………………⑤
当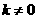 时,
时, ,由④⑤得,
,由④⑤得,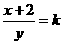 ,将其代入⑤有
,将其代入⑤有
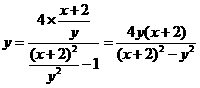 .整理得:
.整理得: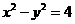 .
.
当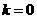 时,点
时,点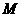 的坐标为
的坐标为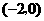 ,满足上述方程.
,满足上述方程.
当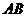 与
与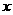 轴垂直时,
轴垂直时,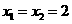 ,求得
,求得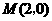 ,也满足上述方程.
,也满足上述方程.
故点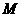 的轨迹方程是
的轨迹方程是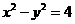 .
.
13 P是△ABC所在平面外一点,O是点P在平面α上的射影,若点P到△ABC的三边的距离相等,则O是△ABC_________心..13内心
14双曲线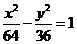 左支上的点P到左准线的距离是10,那么P到其右焦点的距离是
14
左支上的点P到左准线的距离是10,那么P到其右焦点的距离是
14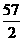
15给出下列四个命题:①异面直线是指空间既不平行又不相交的直线;②两异面直线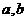 ,如果
,如果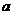 平行于平面
平行于平面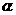 ,那么
,那么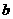 不平行平面
不平行平面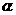 ;③两异面直线
;③两异面直线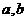 ,如果
,如果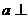 平面
平面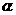 ,那么
,那么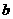 不垂直于平面
不垂直于平面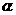 ;④两异面直线在同一平面内的射影不可能是两条平行直线 。其中正确的命题是____________ 15①③
;④两异面直线在同一平面内的射影不可能是两条平行直线 。其中正确的命题是____________ 15①③
16给出下列四个命题:① 两平行直线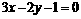 和
和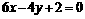 间的距离是
间的距离是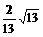 ;② 方程
;② 方程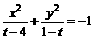 不可能表示圆;③ 若双曲线
不可能表示圆;③ 若双曲线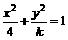 的离心率为e,且
的离心率为e,且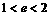 ,则k的取值范围是
,则k的取值范围是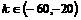 ;④ 曲线
;④ 曲线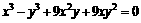 关于原点对称.其中所有正确命题的序号是_____________
. 16 ①,④.
关于原点对称.其中所有正确命题的序号是_____________
. 16 ①,④.
1 (理)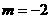 是直线
是直线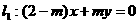 和直线
和直线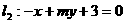 互相垂直的( A
)
互相垂直的( A
)
A.充分而不必要条件B. 必要不充分条件C. 充要条件D.既不充分又不必要条件
2(理)过点(2,-1)作圆x2+y2=5的切线,其方程是( B )
A.x-2y-4=0 B.2x-y-5=0 C.2x+y-3=0 D.2x-y-5=0或x-2y+4=0
3(理)椭圆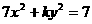 的一个焦点是(0,
的一个焦点是(0,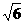 )那么k等于(
B )
)那么k等于(
B )
A. 2 B. 1 C. 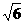 D. 3
D. 3
4空间三条直线互相平行,由每两条平行线确定一个平面,则可确定平面的个数为 (C)
A.3 B.1或2 C.1或3 D.2或3
5(理)动点P到直线x+y-4=0的距离等于它到点M(2,2)的距离,则点P的轨迹是( A )
A.直线 B.椭圆 C.双曲线 D.抛物线
6(理)设双曲线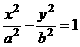 (a>0,b>0)的实轴长、虚轴长、焦距成等比数列,则双曲线的离心率为(B )
(a>0,b>0)的实轴长、虚轴长、焦距成等比数列,则双曲线的离心率为(B )
A.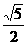 B.
B.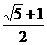 C.
C.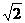 D.
D.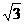
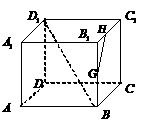
7如图,在正方体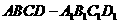 中,
中,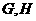 分别为
分别为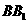 ,
,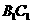 的中点,则异面直线
的中点,则异面直线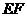 与
与 所成的角等于( B )
所成的角等于( B )
A.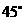 B.
B.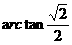 C.
C.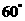 D.
D.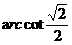
8若双曲线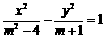 的焦点在y轴上,则m的取值范围是( C
).
的焦点在y轴上,则m的取值范围是( C
).
A.(-2,2) B.(1,2) C.(-2,-1) D.(-1,2)
9. 抛物线y2=4px(p>0)的焦点为F,P为其上的一点,O为坐标原点,若△OPF为等腰三角形,则这样的点P的个数为( .C )
抛物线y2=4px(p>0)的焦点为F,P为其上的一点,O为坐标原点,若△OPF为等腰三角形,则这样的点P的个数为( .C )
A.2 B.3 C.4 D.6
10(理)如图,是一个无盖正方体盒子的表面展开图,A、B、C为其上的三个点,则在正方体盒子中,∠ABC等于 ( B )
A.45° B.60° C.90° D.120°
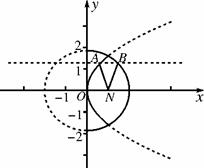 11定点N(1,0),动点A、B分别在图中抛物线y2=4x及椭圆
11定点N(1,0),动点A、B分别在图中抛物线y2=4x及椭圆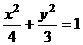 的实线部分上运动,且AB∥x轴,则△NAB的周长l的取值范围是( )
的实线部分上运动,且AB∥x轴,则△NAB的周长l的取值范围是( )
A.(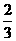 ,2)
B.(
,2)
B.(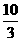 ,4)
,4)
C.(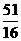 ,4)
D.(2,4)
,4)
D.(2,4)
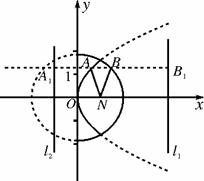 11B 如图所示,分别作出椭圆准线l1:x=4与抛物线的准线l2:x=-1,分别过点A、B作AA1⊥l2于A1,BB1⊥l1于B1,由椭圆的第二定义可得|BN|=e|BB1|=2
11B 如图所示,分别作出椭圆准线l1:x=4与抛物线的准线l2:x=-1,分别过点A、B作AA1⊥l2于A1,BB1⊥l1于B1,由椭圆的第二定义可得|BN|=e|BB1|=2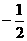 xB,由抛物线定义可得|AN|=|AA1|=xA+1,∴△NAB的周长l=|AN|+|AB|+|BN|
xB,由抛物线定义可得|AN|=|AA1|=xA+1,∴△NAB的周长l=|AN|+|AB|+|BN|
=xA+1+(xB-xA)+(2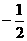 xB)=3+
xB)=3+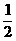 xB,又由
xB,又由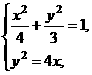 可得两曲线交点的横坐标为x=
可得两曲线交点的横坐标为x=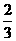 ,∵xB∈(
,∵xB∈(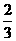 ,2),∴3+
,2),∴3+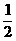 xB∈(
xB∈(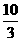 ,4),即△NAB的周长l的取值范围为(
,4),即△NAB的周长l的取值范围为(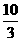 ,4),故应选B.
,4),故应选B.
12点P(-3,1)在椭圆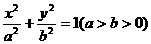 的左准线上,过点P且方向为
的左准线上,过点P且方向为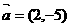 的光线,经直线
的光线,经直线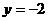 反射后通过椭圆的左焦点,则这个椭圆的离心率为 ( )
反射后通过椭圆的左焦点,则这个椭圆的离心率为 ( )
A.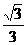 B.
B.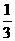 C.
C.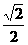 D.
D.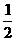
12A 点P(-3,1)在椭圆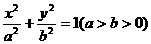 的左准线上, 故
的左准线上, 故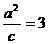
点P(-3,1)关于直线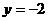 的对称的点为Q,则Q(-3,-5),设椭圆的左焦点为F,则直线FQ为
的对称的点为Q,则Q(-3,-5),设椭圆的左焦点为F,则直线FQ为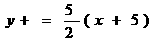 ,故
,故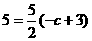
∴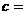 1,
1,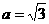
16. 在正方体上任意选择4个顶点,它们可能是如下各种几何形体的4个顶点,这些几何形体
是 (写出所有正确结论的编号)。①矩形;②不是矩形的平行四边形;③有三个面为等
腰直角三角形,有一个面为等边三角形的四面体;④每个面都是等边三角形的四面体;⑤每个面都是直角三
角形的四面体。
 2008年宣威八中
2008年宣威八中
高二数学(理科)检测卷
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com