
题目列表(包括答案和解析)
5.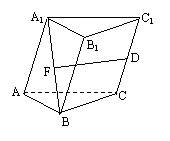 在三棱柱ABC-A1B1C1中,D是CC1的中点,F是A1B的中点,且
在三棱柱ABC-A1B1C1中,D是CC1的中点,F是A1B的中点,且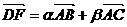 ,则( )
,则( )
A.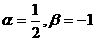
B.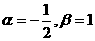
C.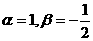
D. 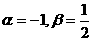
4.过点M(2,4)作直线与抛物线y2=8x只有一个公共点,则这样的直线条数是 ( )
A. 0 B. 1 C. 2 D. 3
3.复数z=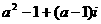 (
(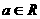 )是纯虚数,则
)是纯虚数,则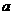 的值为 ( )
的值为 ( )
A. 1
B. 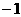 C. 1或
C. 1或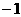 D.
D. 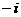
2.若直线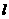 的方向向量为
的方向向量为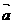 =(1,0,2),平面
=(1,0,2),平面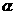 的法向量为
的法向量为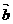 =(-2,0,-4),则 ( )
=(-2,0,-4),则 ( )
A. 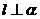 B.
B.
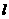 ∥
∥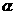 C.
C. 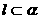 D.
D. 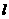 与
与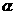 斜交
斜交
1.已知定点F1、F2,且|F1F2|=6,动点P满足|PF1|-|PF2|=6,则动点P的轨迹是 ( )
A. 椭圆 B. 双曲线 C. 线段 D. 射线
(时间:120分钟 满分:150分)
说明:请将答案填写在答卷纸上,考试结束后只交答案卷。
22、我们在下面的表格中填写数值:先将第1行的所有空格填上1;再把一个首项为1,公比为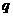 的数列
的数列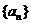 依次填入第一列的空格内;然后按照“任意一格的数是它上面一格的数与它左边一格的数之和”的规则填写其他空格.
依次填入第一列的空格内;然后按照“任意一格的数是它上面一格的数与它左边一格的数之和”的规则填写其他空格.
|
|
第1列 |
第2列 |
第3列 |
…… |
第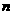 列 列 |
|
第1行 |
1 |
1 |
1 |
…… |
1 |
|
第2行 |
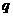 |
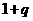 |
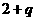 |
|
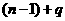 |
|
第3行 |
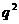 |
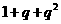 |
|
|
|
|
…… |
…… |
|
|
|
|
第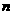 行 行 |
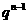 |
 |
|
|
|
(1)按照填写规则,请在上述表格内填写第二行的空格以及第二列的空格;
(2)试用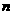 、
、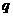 表示第二列的各数之和;
表示第二列的各数之和;
(3)设第3列的数依次为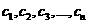 ,若
,若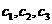 成等比数列,试求
成等比数列,试求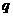 的值;能否找到
的值;能否找到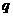 的值,使得数列
的值,使得数列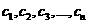 的前
的前 项
项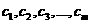
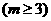 成为等比数列?若能找到,
成为等比数列?若能找到, 的值有多少个?若不能找到,说明理由.
的值有多少个?若不能找到,说明理由.
解:(1)如表……………………………………………………………………3分
(2)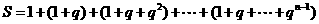
当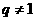 时,
时,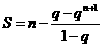 ;……………………………………2分
;……………………………………2分
当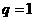 时,
时,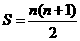 …………………………………………2分
…………………………………………2分
所以综上可知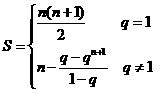 ……………………1分
……………………1分
(5)
可知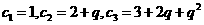
由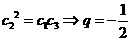 ,则
,则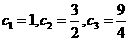
若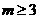 时,
时,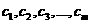 为等比数列,那么
为等比数列,那么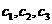 一定是等比数列
一定是等比数列
由上可知此时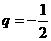 ,又
,又 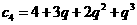 得知
得知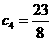
而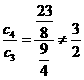 ,所以对于任意的
,所以对于任意的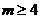 ,
,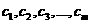 一定不是等比数列
一定不是等比数列
综上所述,当且仅当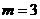 且
且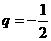 时,数列
时,数列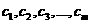 是等比数列.………4分
是等比数列.………4分
21、已知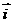 ,
,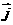 分别是与
分别是与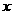 轴,
轴,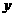 轴正方向相同的单位向量,
轴正方向相同的单位向量,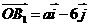
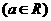 ,对任意正整数
,对任意正整数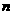 ,
,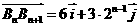 .
.
(1)若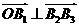 ,求
,求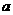 的值;
的值;
(2)求向量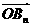 .
.
解:(1)依题可知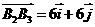
由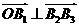 知
知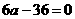 ,所以
,所以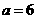 ;…………………………4分
;…………………………4分
(2)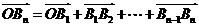 …………………………………………2分
…………………………………………2分
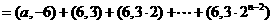
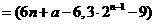
所以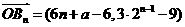 .……………………………………4分
.……………………………………4分
17 已知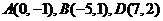 ,且
,且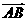 ∥
∥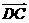 ,
,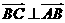 ,求点
,求点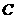 的坐标.
的坐标.
解:设点C 的坐标是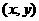 ,
,
则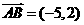 ,
,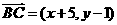 ,
,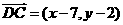 ……………………2分
……………………2分
由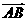 ∥
∥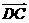
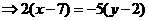
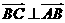
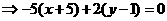 …………………………………………2分
…………………………………………2分
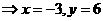 ,所以
,所以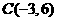 ………………………………………………2分
………………………………………………2分
18 已知一个等差数列的前 项的和是
项的和是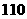 ,前
,前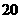 项的和是
项的和是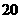 .求此等差数列的前
.求此等差数列的前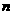 项和
项和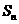 ,并求出当
,并求出当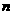 为何值时,
为何值时,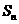 最大,最大值是多少?
最大,最大值是多少?
解:设等差数列的首项为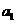 ,公差为
,公差为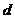 ……………………………………1分
……………………………………1分
则 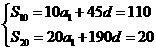 ……………………………………………2分
……………………………………………2分
所以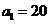 ,
,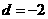
所以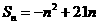 …………………………………………………………2分
…………………………………………………………2分
又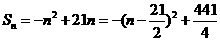 ,
,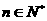
所以当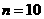 或
或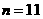 时
时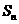 最大,
最大,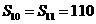 ……………………3分
……………………3分
19设数列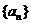 的首项
的首项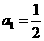 ,且
,且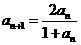 (
(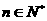 ).(1)求
).(1)求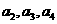 ;
;
(2)根据上述结果猜想数列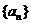 的通项公式,并用数学归纳法加以证明.
的通项公式,并用数学归纳法加以证明.
解:(1)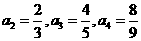 ………………………………………………2分
………………………………………………2分
(2)猜想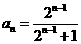 ,(
,(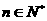 )……………………………………2分
)……………………………………2分
证明:①当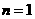 时,左边
时,左边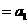 ,右边
,右边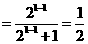 ,猜测成立;
,猜测成立;
②假设当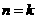 (
(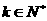 )时有
)时有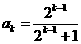 成立
成立
则当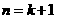 时,左边
时,左边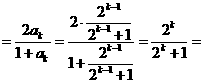 右边.故猜测也成立.
右边.故猜测也成立.
由①②可得对一切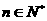 ,数列
,数列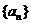 的通项公式为
的通项公式为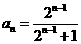 (
(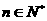 )…………4分
)…………4分
20、在一次人才招聘会上,有甲、乙两家公司分别公布它们的工资标准:
甲公司:第一年月工资数为1500元,以后每年月工资比上一年月工资增加230元;
乙公司:第一年月工资数为2000元,以后每年月工资在上一年的月工资基础上递增5%.
设某人年初同时被甲、乙公司录取,试问:
(3)
若该人打算连续工作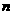 年,则在第
年,则在第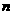 年的月工资收入分别是多少元?
年的月工资收入分别是多少元?
(4) 若该人打算连续工作10年,且只考虑工资收入的总量,该人应该选择哪家公司?为什么?(精确到1元)
解:(1)设在甲公司第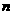 年的工资收入为
年的工资收入为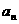 元,在乙公司第
元,在乙公司第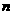 年的工资收入为
年的工资收入为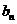 元
元
则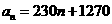 ,
,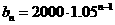 ………………………………4分
………………………………4分
(2)设工作10年在甲公司的总收入为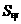 ,在甲公司的总收入为
,在甲公司的总收入为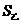
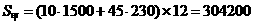
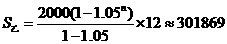
由于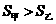 ,所以该人应该选择甲公司.…………………………4分
,所以该人应该选择甲公司.…………………………4分
16、在△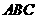 中,有命题①若
中,有命题①若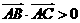 ,则△
,则△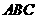 为锐角三角形②
为锐角三角形②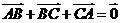 ③
③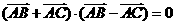 ,则△
,则△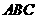 为等腰三角形 ④
为等腰三角形 ④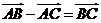 .上述命题正确的是…………………………………………………………………………………………( C )
.上述命题正确的是…………………………………………………………………………………………( C )
A.①② B. ①④ C. ②③ D. ②③④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com