
题目列表(包括答案和解析)
1.有下列命题:① 年
年 月
月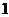 日是国庆节,又是中秋节;②
日是国庆节,又是中秋节;② 的倍数一定是
的倍数一定是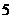 的倍数;
的倍数;
③梯形不是矩形;④方程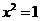 的解
的解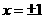 。其中使用逻辑联结词的命题有( )
。其中使用逻辑联结词的命题有( )
A.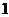 个 B.
个 B.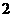 个 C.
个 C.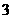 个 D.
个 D.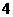 个
个
17已知圆x2+y2=1,直线y=x+m. (1)m为何值时,直线与圆有两个不同的交点?
(2)设直线与圆交于A,B,且直线OA,OB(O为坐标原点)与x轴的正半轴所成的角为α,β,求证:sin(α+β)是与m无关的定值.
17解(1)直线的方程代入圆的方程,可得2x2+2mx+m2-1=0,由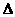 >1,可得4m2-8(m2-1)>0
>1,可得4m2-8(m2-1)>0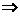 -
-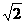 <m<
<m<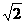 .
.
(2)设A(x1,y1),B(x2,y2),则sinα=y1,cosα=x1,sinβ=y2,cosβ=x2,又y1=x1+m,y2=x2+m,2x2+2mx+m2-1=0,所以x1+x2=-m,x1·x2=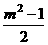 .
.
所以,sin(α+β)=x2y1+x1y2=2x1x2+m(x1+x2)=m2-1+m(-m)=-1(定值).
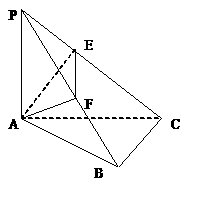 18在空间四边形PABC中,PA
18在空间四边形PABC中,PA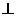 面ABC,AC
面ABC,AC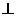 BC,若A在PB,PC上的射影分别是E,F.求证:EF
BC,若A在PB,PC上的射影分别是E,F.求证:EF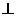 PB
PB
18证明: PA
PA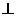 面ABC
面ABC  PA
PA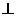 BC--1分,又
BC--1分,又 AC
AC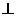 BC,PA
BC,PA AC=A,
AC=A,  BC
BC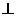 面PAC-----4分,
面PAC-----4分, AF
AF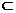 面PAC,
面PAC,  BC
BC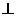 AF-------5分,又
AF-------5分,又 F是点A在PC上的射影,
F是点A在PC上的射影, AF
AF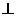 PC--6分,
PC--6分, AF
AF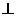 面PBC------8分,
面PBC------8分, AE在平面PBC上的射影为EF-----9分,
AE在平面PBC上的射影为EF-----9分, E是A点在PB上的射影--10分,
E是A点在PB上的射影--10分, AE
AE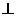 PB
PB  EF
EF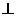 PB----12分
PB----12分
19已知椭圆的中心在原点,焦点在x轴上,一条准线的方程为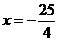 ,焦点到相应准线的距离为
,焦点到相应准线的距离为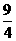 . (1)求该椭圆的标准方程;(2)写出该椭圆的长轴长,短轴长,离心率,焦点坐标和顶点坐标;
(3)求以已知椭圆的焦点为顶点,而以椭圆的顶点为焦点的双曲线方程.
. (1)求该椭圆的标准方程;(2)写出该椭圆的长轴长,短轴长,离心率,焦点坐标和顶点坐标;
(3)求以已知椭圆的焦点为顶点,而以椭圆的顶点为焦点的双曲线方程.
19解:(1)设椭圆的标准方程是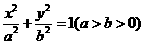 ,则
,则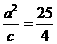 ……①,
……①,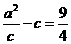 ……②联立①②解得
……②联立①②解得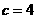 ,
,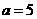 ,所以
,所以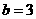 ,故所求的椭圆方程为
,故所求的椭圆方程为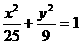 .
.
(2)椭圆的长轴长为10,短轴长为6,离心率为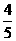 ,焦点坐标为(-4,0),(4,0),顶点坐标为(-5,0),(5,0),(0,-3),(0,3).
,焦点坐标为(-4,0),(4,0),顶点坐标为(-5,0),(5,0),(0,-3),(0,3).
(3)可设双曲线的方程为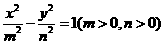 ,由于以已知椭圆的焦点为顶点,而以椭圆的顶点为焦点,故
,由于以已知椭圆的焦点为顶点,而以椭圆的顶点为焦点,故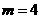 且
且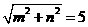 ,所以
,所以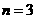 .所求双曲线方程是
.所求双曲线方程是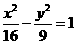 .
.
20已知抛物线的顶点在原点,它的准线经过双曲线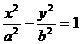 的左焦点,且与x轴垂直,抛物线与此双曲线交于点(
的左焦点,且与x轴垂直,抛物线与此双曲线交于点(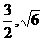 ),求抛物线与双曲线的方程.
),求抛物线与双曲线的方程.
20解:由题意可知抛物线的焦点到准线间的距离为2C(即双曲线的焦距).设抛物线的方程为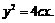 4分
4分
∵抛物线过点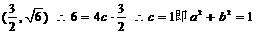 ①
①
又知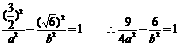 ② 8分
② 8分
由①②可得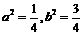 , 10分
, 10分
∴所求抛物线的方程为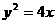 ,双曲线的方程为
,双曲线的方程为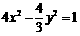 .··· 12分
.··· 12分
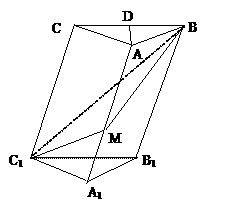 21在斜三棱柱A1B1C1-ABC中, 底面是等腰三角形
21在斜三棱柱A1B1C1-ABC中, 底面是等腰三角形
, AB=AC, 侧面BB1C1C⊥底面ABC.
(Ⅰ)若D是BC的中点, 求证:AD⊥CC1;
(Ⅱ)过侧面BB1C1C的对角线BC1的平面交侧棱
于M, 若AM=MA1, 求证:截面MBC1⊥侧面BB1C1C;
(Ⅲ) AM=MA1是截面MBC1⊥平面BB1C1C的充要
条件吗? 请你叙述判断理由.
21 (Ⅰ)证明: ∵AB=AC, D是BC的中点, ∴AD⊥BC. ∵底面ABC⊥平面BB1C1C, ∴AD⊥侧面BB1C1C. ∴AD⊥CC1.
(Ⅱ)延长B1A1与BM交于N, 连结C1N. ∵AM=MA1, ∴NA1=A1B1. ∵A1B1=A1C1, ∴A1C1= A1N=A1B1. ∴C1N⊥C1B1. ∵截面N B1C1⊥侧面BB1C1C,
∴C1N⊥侧面BB1C1C. ∴截面C1N B⊥侧面BB1C1C. ∴截面MBC1⊥侧面BB1C1C.
(Ⅲ)解: 结论是肯定的, 充分性已由(2)证明,
下面证必要性: 过M作ME⊥B C1于E, ∵截面MBC1⊥侧面BB1C1C, ∴ME⊥侧面BB1C1C. 又∵AD⊥侧面BB1C1C, ∴ME∥AD. ∴M, E, A, D共线. ∵A M∥侧面BB1C1C,
∴AM∥DE. ∵CC1⊥AM, ∴DE∥CC1. ∵D是BC的中点, ∴E是BC1的中点. ∴AM= DE=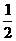 CC1=
CC1=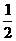 AA1. ∴AM= MA1.
AA1. ∴AM= MA1.
22(文)如图所示,在直角梯形ABCD中,|AD|=3,|AB|=4,|BC|=,曲线段DE上任一点到A、B两点的距离之和都相等.(1)建立适当的直角坐标系,求曲线段DE的方程;
(2)过C能否作一条直线与曲线段DE相交,且所得弦以C为中点,如果能,求该弦所在的直线的方程;若不能,说明理由.
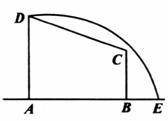 22解:(1)以直线AB为x轴,线段AB的中点为原点建立直角坐标系,则A(-2,0),B(2,0),C(2, ),D(-2,3).依题意,曲线段DE是以A、B为焦点的椭圆的一部分.
22解:(1)以直线AB为x轴,线段AB的中点为原点建立直角坐标系,则A(-2,0),B(2,0),C(2, ),D(-2,3).依题意,曲线段DE是以A、B为焦点的椭圆的一部分.

(2)设这样的弦存在,其方程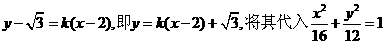
得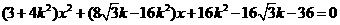
设弦的端点为M(x1,y1),N(x2,y2),则由
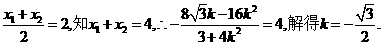
∴弦MN所在直线方程为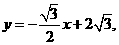 验证得知,这时
验证得知,这时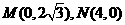 适合条件.故这样的直线存在,其方程为
适合条件.故这样的直线存在,其方程为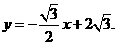
13 P是△ABC所在平面外一点,O是点P在平面α上的射影,若点P到△ABC的三边的距离相等,则O是△ABC_________心..13内心
14双曲线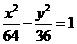 左支上的点P到左准线的距离是10,那么P到其右焦点的距离是
14
左支上的点P到左准线的距离是10,那么P到其右焦点的距离是
14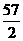
15给出下列四个命题:①异面直线是指空间既不平行又不相交的直线;②两异面直线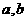 ,如果
,如果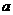 平行于平面
平行于平面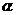 ,那么
,那么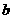 不平行平面
不平行平面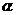 ;③两异面直线
;③两异面直线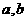 ,如果
,如果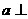 平面
平面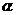 ,那么
,那么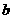 不垂直于平面
不垂直于平面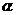 ;④两异面直线在同一平面内的射影不可能是两条平行直线 。其中正确的命题是____________ 15①③
;④两异面直线在同一平面内的射影不可能是两条平行直线 。其中正确的命题是____________ 15①③
16给出下列四个命题:① 两平行直线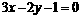 和
和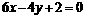 间的距离是
间的距离是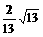 ;② 方程
;② 方程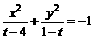 不可能表示圆;③ 若双曲线
不可能表示圆;③ 若双曲线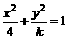 的离心率为e,且
的离心率为e,且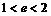 ,则k的取值范围是
,则k的取值范围是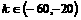 ;④ 曲线
;④ 曲线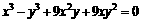 关于原点对称.其中所有正确命题的序号是_____________
. 16 ①,④.
关于原点对称.其中所有正确命题的序号是_____________
. 16 ①,④.
1(文)两直线2x – y + k = 0 与4x – 2y + 1 = 0的位置关系为( D ).
A.平行 B.垂直 C.相交但不垂直 D.平行或重合
2(文)圆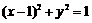 的圆心到直线
的圆心到直线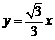 的距离是( A
).
的距离是( A
).
A.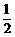 B.
B.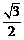 C.1 D.
C.1 D.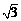
3(文)椭圆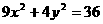 的焦点坐标是( C )
的焦点坐标是( C )
A.(±3,0) B.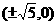 C.
C. 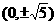 D. (0,±3)
D. (0,±3)
4空间三条直线互相平行,由每两条平行线确定一个平面,则可确定平面的个数为 (C)
A.3 B.1或2 C.1或3 D.2或3
5(文)若A是定直线l外的一定点,则过A且与l相切圆的圆心轨迹是( B ).
A.圆 B.抛物线 C.椭圆 D.双曲线一支
6(文)设M为双曲线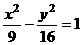 上位于第四象限内的一点,F1,F2是两个焦点,且有MF1∶MF2=1∶3,则△MF1F2的周长等于(B )
上位于第四象限内的一点,F1,F2是两个焦点,且有MF1∶MF2=1∶3,则△MF1F2的周长等于(B )
A.16 B.22 C.26 D.30
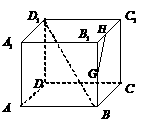 7如图,在正方体
7如图,在正方体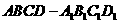 中,
中,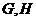 分别为
分别为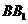 ,
,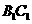 的中点,则异面直线
的中点,则异面直线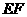 与
与 所成的角等于( B )
所成的角等于( B )
A. B.
B.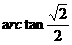 C.
C.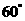 D.
D.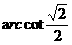
8若双曲线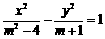 的焦点在y轴上,则m的取值范围是( C
).
的焦点在y轴上,则m的取值范围是( C
).
A.(-2,2) B.(1,2) C.(-2,-1) D.(-1,2)
9.抛物线y2=4px(p>0)的焦点为F,P为其上的一点,O为坐标原点,若△OPF为等腰三角形,则这样的点P的个数为( .C )
A.2 B.3 C.4 D.6
10(文)若RtΔABC的直角边AB与平面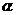 平行,另一直角边BC与
平行,另一直角边BC与 斜交,则∠ABC在
斜交,则∠ABC在 上的射影
(D )
上的射影
(D )
A.是一条射线 B.是钝角 C.是锐角 D.是直角
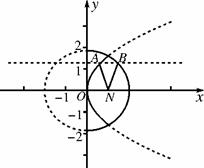 11定点N(1,0),动点A、B分别在图中抛物线y2=4x及椭圆
11定点N(1,0),动点A、B分别在图中抛物线y2=4x及椭圆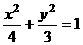 的实线部分上运动,且AB∥x轴,则△NAB的周长l的取值范围是( )
的实线部分上运动,且AB∥x轴,则△NAB的周长l的取值范围是( )
A.(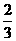 ,2)
B.(
,2)
B.(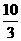 ,4)
,4)
C.(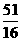 ,4)
D.(2,4)
,4)
D.(2,4)
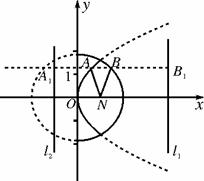 11B 如图所示,分别作出椭圆准线l1:x=4与抛物线的准线l2:x=-1,分别过点A、B作AA1⊥l2于A1,BB1⊥l1于B1,由椭圆的第二定义可得|BN|=e|BB1|=2
11B 如图所示,分别作出椭圆准线l1:x=4与抛物线的准线l2:x=-1,分别过点A、B作AA1⊥l2于A1,BB1⊥l1于B1,由椭圆的第二定义可得|BN|=e|BB1|=2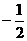 xB,由抛物线定义可得|AN|=|AA1|=xA+1,∴△NAB的周长l=|AN|+|AB|+|BN|
xB,由抛物线定义可得|AN|=|AA1|=xA+1,∴△NAB的周长l=|AN|+|AB|+|BN|
=xA+1+(xB-xA)+(2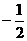 xB)=3+
xB)=3+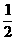 xB,又由
xB,又由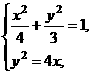 可得两曲线交点的横坐标为x=
可得两曲线交点的横坐标为x=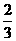 ,∵xB∈(
,∵xB∈(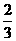 ,2),∴3+
,2),∴3+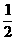 xB∈(
xB∈(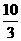 ,4),即△NAB的周长l的取值范围为(
,4),即△NAB的周长l的取值范围为(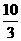 ,4),故应选B.
,4),故应选B.
12点P(-3,1)在椭圆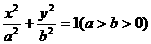 的左准线上,过点P且方向为
的左准线上,过点P且方向为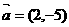 的光线,经直线
的光线,经直线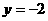 反射后通过椭圆的左焦点,则这个椭圆的离心率为 ( )
反射后通过椭圆的左焦点,则这个椭圆的离心率为 ( )
A.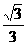 B.
B.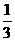 C.
C.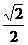 D.
D.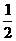
12A 点P(-3,1)在椭圆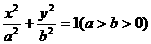 的左准线上, 故
的左准线上, 故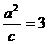
点P(-3,1)关于直线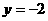 的对称的点为Q,则Q(-3,-5),设椭圆的左焦点为F,则直线FQ为
的对称的点为Q,则Q(-3,-5),设椭圆的左焦点为F,则直线FQ为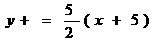 ,故
,故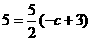
∴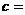 1,
1,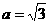
22、(14分)已知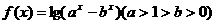
(1)求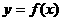 的定义域;
的定义域;
(2)在函数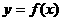 的图象上是否存在不同的两点,使经过这两点的直线平行
的图象上是否存在不同的两点,使经过这两点的直线平行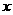 轴;
轴;
(3)当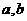 满足什么条件时,
满足什么条件时,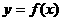 在区间
在区间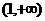 上恒取正值。
上恒取正值。
“华安、连城、永安、漳平一中,龙海二中” 五校联考
 2007-2008学年下学期第一次月考
2007-2008学年下学期第一次月考
21、(12分)某服装厂生产一种服装,每件服装的成本为40元,出厂单价定为60元,为鼓励销售商订购,决定当一次订购量超过100件时,每多订购一件,订购的全部服装的出厂单价就降低0.02元,根据市场调查,销售商一次订购量不会超过500件。
(1)设一次订购量为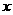 件,服装的实际出厂单价为
件,服装的实际出厂单价为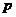 元,写出函数
元,写出函数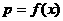 的表达式;
的表达式;
(2)当销售商一次订购450件服装时,该服装厂获得的利润是多少元?(服装厂售出一件服装的利润=实际出厂价-成本)
20、(12分)已知函数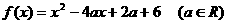
(1)若函数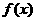 的值域为
的值域为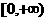 求
求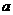 的值;
的值;
(2)若函数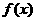 的值都是非负数,求函数
的值都是非负数,求函数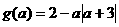 的值域。
的值域。
19、(12分)设甲、乙两人每次射击命中目标的概率分别为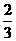 和
和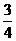 ,且各次射击相互独立。
,且各次射击相互独立。
(1)若甲、乙各射击一次,求甲命中但乙未命中目标的概率;
(2)若甲、乙各射击两次,求甲命中目标的次数大于乙命中目标次数的概率。
18、(12分)已知函数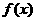 定义域为(-2,2),函数
定义域为(-2,2),函数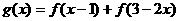
(1)求函数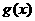 的定义域;
的定义域;
(2)若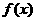 是奇函数且在定义域上单调递减,求不等式
是奇函数且在定义域上单调递减,求不等式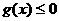 的解集。
的解集。
17、(12分)已知复数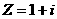
(1)求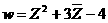
(2)如果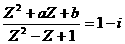 求实数
求实数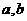
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com