
题目列表(包括答案和解析)
22.
已知数列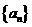 满足
满足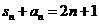 ,
,
( 1 ) 写出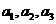 ,并推测
,并推测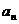 的表达式;
的表达式;
( 2 ) 用数学归纳法证明所得的结论。
(3 ) 把数列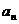 的所有数按照从小到大的
的所有数按照从小到大的
序号、左小右大的原则写成如右数表:
第k行有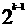 个数,第t行的第s个数
个数,第t行的第s个数
(从左数起)记为A(t,s),求通项公式A(t,s)(用t,s来表示)
21.
已知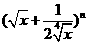 的展开式中前三项系数成等差数列。
的展开式中前三项系数成等差数列。
(1)展开式里所有的x的有理项;
(2)求展开式里系数最大的项。

20.
(1)用分析法证明: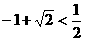
(2)用反证法证明:如果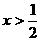 ,那么
,那么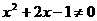 。
。
19.
袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为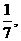 现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时既终止,每个球在每一次被取出的机会是等可能的,用
现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时既终止,每个球在每一次被取出的机会是等可能的,用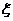 表示取球终止所需要的取球次数.
表示取球终止所需要的取球次数.
(1)求袋中所有的白球的个数;
(2)求随机变量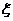 的概率分布;
的概率分布;
18. 下列四个类比推理得到的结果不正确的是 (写出所有不正确的序号)
① 平面内正三角形的“三边相等,三内角相等”的性质可类比正四体各个面都是全等的正三角形,相邻两个面所成的二面角相等;
②
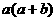 =
=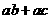 类比
类比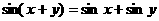
③ 若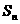 是等差数列
是等差数列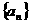 的前
的前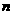 项和,公差为
项和,公差为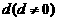 ,则数列
,则数列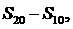
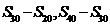 也成等差数列,且公差为
也成等差数列,且公差为 ,类比若
,类比若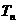 是等比数列
是等比数列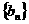
的前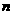 项积,公比为
项积,公比为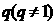 ,则有
,则有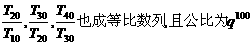 .
.
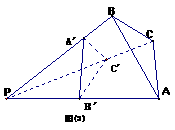
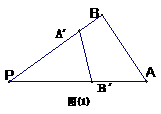
④ 由图(1)有面积关系: 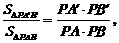
则由(2)
有体积关系: 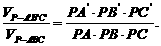
17. 三行三列的方阵中有9个不同的数,从中任取三个数,则至少有两个数位于同行或同列有 种不同的方法。
16.
将数字1,2,3,4,5,6拼成一列,记第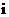 个数为
个数为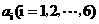 ,若
,若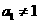 ,
,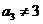 ,
,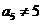 ,
,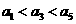 ,则不同的排列方法有 种(用数字作答).
,则不同的排列方法有 种(用数字作答).
15.
幻方就是把1,2,3,……,n2排成一个n行n列的方阵,使得每行中的各数之和、每列中的各数之和以及两条对角线中的各数之和都是同一个数 ,称作“n阶幻方”,数
,称作“n阶幻方”,数 称为“幻和”。则
称为“幻和”。则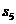 =
.
=
.
14.
从不同号码的4双鞋中任取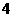 只,其中恰好有
只,其中恰好有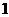 双的取法种数为
双的取法种数为
13.
设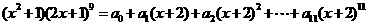 ,则
,则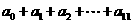 的值为
的值为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com