
题目列表(包括答案和解析)
22.(本小题满分14分)已知点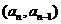 在曲线
在曲线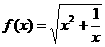 上, 且
上, 且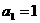 .
.
(1)求f(x)的定义域;
(2)求证: 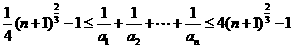 (n∈N*)
(n∈N*)
21.(本小题满分15分)平面直角坐标系中,O为坐标原点,已知两定点A(1,0),B(0,-1),动点
P(x,y)满足: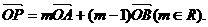
⑴求点P的轨迹方程;
⑵设点P的轨迹与双曲线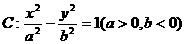 交于相异两点M、N,若以MN为直径的圆经过原点,且双曲线C的离心率等于
交于相异两点M、N,若以MN为直径的圆经过原点,且双曲线C的离心率等于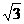 ,求双曲线C的方程.
,求双曲线C的方程.
20.(本小题满分15分)已知函数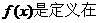 [-2,2]上的奇函数,当
[-2,2]上的奇函数,当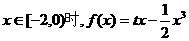 (t为常数).
(t为常数).
⑴求函数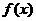 的解析式;
的解析式;
⑵当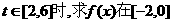 上的最小值以及取得最小值时的x值;
上的最小值以及取得最小值时的x值;
⑶当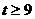 时,证明函数
时,证明函数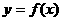 的图像至少有一个点落在直线
的图像至少有一个点落在直线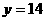 上.
上.
18.(本小题满分14分)
甲乙两队参加奥运知识竞赛,每队3人,每人回答一个问题,答对者为本队赢得一分,
答错得零分。假设甲队中每人答对的概率均为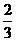 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为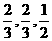 且各人正确与否相互之间没有影响.用ε表示甲队的总得分.
且各人正确与否相互之间没有影响.用ε表示甲队的总得分.
(Ⅰ)求随机变量ε分布列和数学期望;
(Ⅱ)用A表示“甲、乙两个队总得分之和等于3”这一事件,用B表示“甲队总得分大于乙队总得分”这一事件,求P(AB).
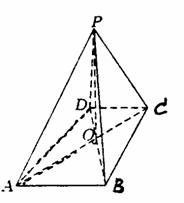 19.(本题满分14分)如图,已知四棱锥P-ABCD的底面ABCD为等腰梯形,AB//CD,AC⊥DB,AC与BD相交于点O,且顶点P在底面上的射影恰为O点,又BO=2,PO=
19.(本题满分14分)如图,已知四棱锥P-ABCD的底面ABCD为等腰梯形,AB//CD,AC⊥DB,AC与BD相交于点O,且顶点P在底面上的射影恰为O点,又BO=2,PO=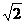 ,PB⊥PD.
,PB⊥PD.
⑴求异面直线PD与BC所成角的余弦值;
⑵求二面角P-AB-C的大小;
⑶设点M在棱PC上,且 ,问
,问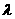 为何值时,
为何值时,
PC⊥平面BMD.
17.如图是某条公共汽车线路收支差额y与乘客量x
|
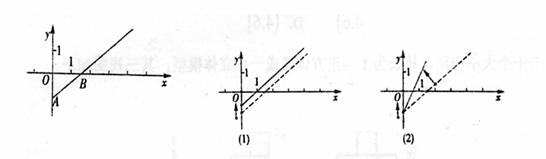 用).由于目前本条线路亏损,公司有关人员分别将右图移动为下图(1)和图(2),从
用).由于目前本条线路亏损,公司有关人员分别将右图移动为下图(1)和图(2),从
而提出了两种扭亏为盈的建议.
请你根据图像用简练的语言叙述出:
建议⑴是 ▲
建议⑵是 ▲
16.设函数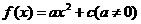 .若
.若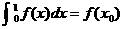 ,0≤x0≤1,则x0的值为 ▲ .
,0≤x0≤1,则x0的值为 ▲ .
15.若数列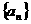 的通项公式
的通项公式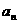 =
=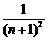 ,记
,记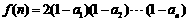 ,试通过计算
,试通过计算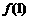 ,
,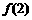 ,
,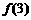 的值,推测出
的值,推测出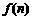 = ▲ .
= ▲ .
14.在△ABC中,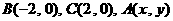 ,给出△ABC满足的条件,就能得到动点A的轨迹方程,下表给出了一些条件及方程:
,给出△ABC满足的条件,就能得到动点A的轨迹方程,下表给出了一些条件及方程:
|
条件 |
方程 |
|
①△ABC周长为10 |
 : :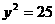 |
|
②△ABC面积为10 |
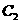 : :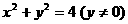 |
|
③△ABC中,∠A=90° |
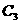 : : |
则满足条件①、②、③的轨迹方程分别为 ▲
(用代号 、
、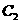 、
、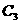 填入)
填入)
13.如果复数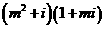 是实数,则实数
是实数,则实数 =_______▲_______.
=_______▲_______.
12.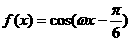 最小正周期为
最小正周期为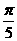 ,其中
,其中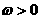 ,则
,则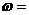 ▲
▲
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com