
题目列表(包括答案和解析)
12.(文科)由题设和焦半径公式得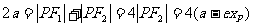 .
.
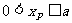 .∴
.∴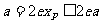 .即
.即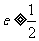 .选(B).
.选(B).
(理科)不妨设右准线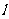 交
交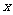 轴于点A,由平几知识知过E、F的圆且与
轴于点A,由平几知识知过E、F的圆且与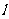 相切于点P时,∠EPF最大.由圆幂定理得
相切于点P时,∠EPF最大.由圆幂定理得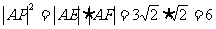 .
.
易得∠FPA=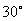 ,∠EPA=
,∠EPA=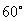 ,从而∠EPF=
,从而∠EPF=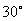 为所求最大值,故选(B).
为所求最大值,故选(B).
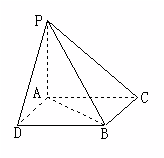
11.如图,过B作BD∥CA,且满足BD=CA,
则∠PBD为PB与AC所成的角.
易得四边形ADBC为正方形,
由PA⊥平面ABC得BD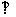 PD.
PD.
在Rt△PDB中,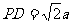 ,
,
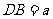 ,
,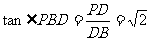 .选(B).
.选(B).
10.由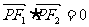 得
得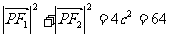 ,
,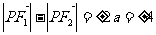 .
.
 ∴
∴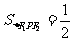
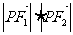 =12.选(D).
=12.选(D).
9.(文科)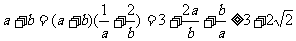 ,选(B).
,选(B).
(理科)令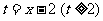 ,则
,则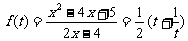 .
.
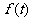 在
在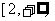 上是单调递增函数,故
上是单调递增函数,故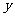 的最小值是
的最小值是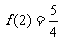 .选(B).
.选(B).
8.点A在抛物线含焦点区域,过A作AP垂直于抛物线的准线交抛物线于点P,则由抛物线的定义知点P(2,2)为所求点.选(B).
7.设截得的弦为AB,圆心为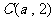 ,作
,作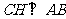 于H,则由平几知识得
于H,则由平几知识得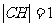 .
.
由此得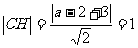 ,解得
,解得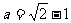 .选(C).
.选(C).
6.由A(1,4)、B(3,1)在直线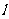 上或其异侧得
上或其异侧得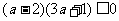 .
.
解得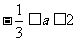 .选(B).
.选(B).
5.由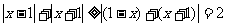 知
知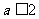 .选(B).
.选(B).
4.(文科)①、④正确,选(C).
(理科)对于任意的直线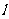 与平面
与平面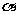 ,若
,若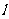 在平面
在平面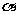 内,则存在直线m⊥
内,则存在直线m⊥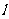 ;
;
若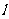 不在平面
不在平面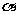 内,且
内,且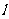 ⊥
⊥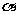 ,则平面
,则平面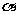 内任意一条直线都垂直于
内任意一条直线都垂直于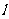 ;
;
若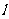 不在平面
不在平面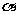 内,且
内,且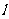 与
与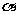 不垂直,则它的射影在平面
不垂直,则它的射影在平面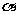 内为一条直线,在平面
内为一条直线,在平面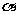 内必有直线
内必有直线 垂直于它的射影,则
垂直于它的射影,则 ⊥
⊥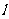 .故选(C).
.故选(C).
3.由题设知动点P到定点(1,0)的距离和它到定直线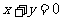 的距离的比是常数
的距离的比是常数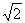 ,根据双曲线的第二定义可得点P的轨迹为双曲线.选(B).
,根据双曲线的第二定义可得点P的轨迹为双曲线.选(B).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com