
8.已知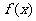 是定义在
是定义在 上的偶函数,且在
上的偶函数,且在 上是增函数,设
上是增函数,设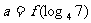 ,
,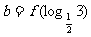 ,
,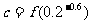 ,则
,则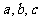 的大小关系是 ( )
的大小关系是 ( )
A.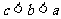 B.
B.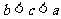 C.
C. D.
D.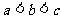
7.已知函数y= (
(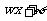 )+k的最大值是4,最小值是0,最小正周期是
)+k的最大值是4,最小值是0,最小正周期是 ,直线
,直线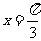 是其图象的一条对称轴,则下面各式中符合条件的解析式是 ( )
是其图象的一条对称轴,则下面各式中符合条件的解析式是 ( )
A.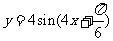 B.
B.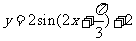
C.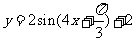 D.
D.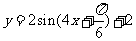
6.已知 、
、 是平面,
是平面, 、
、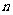 是直线,给出下列命题:①若
是直线,给出下列命题:①若 ,
,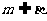 ,则
,则 。
。
②如果 是异面直线,那么
是异面直线,那么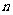 不与
不与 相交.③若
相交.③若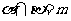 ,
,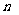 ∥
∥ ,且
,且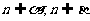 ,则
,则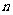 ∥
∥ 且
且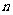 ∥
∥ .其中真命题的个数是 ( )
.其中真命题的个数是 ( )
A.3 B.2 C.1 D.0
5.数列{an}满足a1+
3·a2+ 32·a3+…+ 3n-1·an=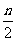 ,则an= ( )
,则an= ( )
A. B.
B. C.
C. D.
D.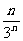
4.函数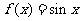 在区间
在区间 上是增函数,且
上是增函数,且 ,则
,则 的值为
的值为
( )
A.0 B. C.1 D.-1
C.1 D.-1
3.若复数z满足对应关系f(1-z)=2z-i,则(1+i)·f(1-i)= ( )
A.2 B. C.
C. D.0
D.0
2.已知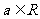 ,则“
,则“ ”是“
”是“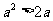 ”的 ( )
”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
1.已知集合P={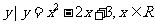 },Q={
},Q={ },则
},则 ( )
( )
A.R B.(-2,+ ) C.
) C.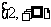 D.
D.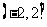
22.(本小题满分14分)已知函数f(x)=x3+ax2+bx+c的图象经过原点,且在x=1处取得极大值。
(1)求实数 的取值范围;
的取值范围;
(2)若方程 恰好有两个不同的根,求
恰好有两个不同的根,求 的解析式;
的解析式;
(3)对于(2)中的函数 ,若对于任意实数α和β恒有不等式
,若对于任意实数α和β恒有不等式
 成立,求m的最小值.
成立,求m的最小值.
21.(本小题满分12分)
已知点 的坐标为
的坐标为 ,点
,点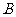 为
为 轴负半轴上的动点,以线段
轴负半轴上的动点,以线段 为边作菱形
为边作菱形 ,使其两对角线的交点恰好在
,使其两对角线的交点恰好在 轴上。
轴上。
(1)求动点 的轨迹E的方程;
的轨迹E的方程;
(2)若点 是(1)中轨迹E上的动点,点
是(1)中轨迹E上的动点,点 是定点,是否存在垂直
是定点,是否存在垂直 轴的直线
轴的直线 ,使得直线
,使得直线 被以线段
被以线段 为直径的圆截得的弦长恒为定值?若存在,用
为直径的圆截得的弦长恒为定值?若存在,用 表示直线
表示直线 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com