
2.无穷数列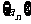 满足:
满足: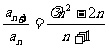 (
(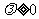 为常数).
为常数).
(1)若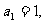 且数列
且数列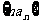 为等比数列,求
为等比数列,求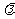 ;
;
(2)已知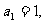
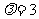 ,若
,若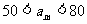 ,求
,求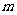 ;
;
(3)若存在正整数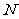 ,使得当
,使得当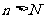 时,有
时,有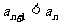 ,求证:存在正整数
,求证:存在正整数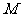 ,使得当
,使得当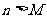 时,有
时,有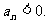
命题意图:
数列中涉及恒成立或存在性的问题,往往和最大(小)值及单调性有关,常见做法是用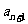 和
和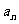 进行作差、作商、比较或构造函数来判断;通过本题的练习,希望学生能根据题目的条件和结论获取信息,抓住特点,进行代数推理论证;本题第(3)问也可用反证法说明,解题中要重视它的运用.
进行作差、作商、比较或构造函数来判断;通过本题的练习,希望学生能根据题目的条件和结论获取信息,抓住特点,进行代数推理论证;本题第(3)问也可用反证法说明,解题中要重视它的运用.
立体几何
1.设数列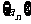 的前
的前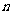 项和为
项和为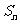 ,且满足
,且满足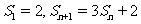
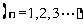 .
.
(Ⅰ)求证:数列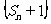 为等比数列;
为等比数列;
(Ⅱ)求通项公式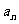 ;
;
(Ⅲ)设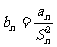 ,求证:
,求证: .
.
命题意图:
数列既是高中数学的重点,也是难点,掌握好等差、等比数列的通项公式和前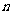 项和公式,能用概念判断是否为等差、等比数列。常见考点:
项和公式,能用概念判断是否为等差、等比数列。常见考点: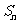 与
与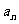 的关系(注意讨论);
的关系(注意讨论);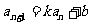 ;递推--猜想--数学归纳法证明;迭加
;递推--猜想--数学归纳法证明;迭加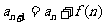 ;迭乘
;迭乘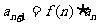 ;裂项求和;错位相减等;数列不等式证明中注意放缩法的运用.
;裂项求和;错位相减等;数列不等式证明中注意放缩法的运用.
2.已知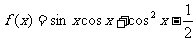 .
.
(1)求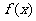 的对称轴方程;
的对称轴方程;
(2)将函数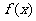 的图象按向量
的图象按向量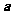 平移后得到函数
平移后得到函数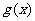 的图象,若
的图象,若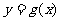 的图象关于点
的图象关于点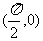 对称,求
对称,求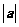 的最小值.
的最小值.
命题意图:
对于三角公式,重中之重是倍角公式、降幂公式及辅助角公式.如果三角函数解答题要求单调性、对称性、周期等,一般暗示着“化一”的过程,即通过恒等变形把函数化为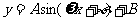 ;另外会从“数”和“形”两方面来分析这个函数的性质和几何特点,即以图引导思维;注意平移问题的处理,如函数平移,按向量平移,曲线的平移问题.
;另外会从“数”和“形”两方面来分析这个函数的性质和几何特点,即以图引导思维;注意平移问题的处理,如函数平移,按向量平移,曲线的平移问题.
提示:要求学生记清诱导公式,“特殊角”的三角函数值.
数列
1.在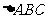 中,
中,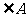 、
、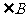 、
、 所对的边长分别是
所对的边长分别是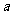 、
、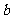 、
、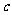 .满足
.满足 .
.
(1)求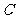 的大小;
的大小;
(2)求 的最大值.
的最大值.
命题意图:
在已知边角关系中既有边又有角的等式,一般要进行边角统一,边化角常用正弦定理,角化边常用正弦、余弦定理;熟练掌握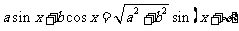 的变形;另外对于函数
的变形;另外对于函数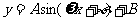 的图象和性质要掌握好;已知三角函数值求角时,一定要注意角的取值范围,注意细节.
的图象和性质要掌握好;已知三角函数值求角时,一定要注意角的取值范围,注意细节.
21.(12分)
已知函数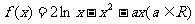
(1)当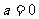 时,求函数
时,求函数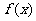 的极值;
的极值;
(2)设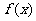 的图象与x轴交于
的图象与x轴交于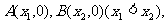 线段AB的中点为
线段AB的中点为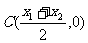 ,过点C作平行于y轴的直线交
,过点C作平行于y轴的直线交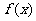 于点D,求证:函数
于点D,求证:函数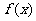 在点D的切线与y轴不垂直;
在点D的切线与y轴不垂直;
(3)证明: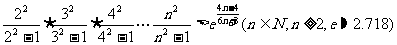
20.(12分)
已知曲线C上任意一点M到点F(0,1)的距离比它到直线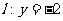 的距离小1。
的距离小1。
(1)求曲线C的方程;
(2)若过点P(2,2)的直线m与曲线C交于A,B两点,设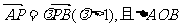 的面积为
的面积为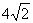 ,(O为坐标原点),求实数
,(O为坐标原点),求实数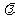 的值。
的值。
19.(12分)
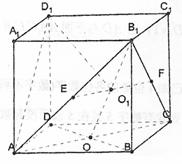
正四棱柱ABCD-A1B1C1D1中,底面边长为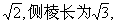 E,F分别是AB1,CB1的中点,O为AC中点,连接B1O交EF于O1,
E,F分别是AB1,CB1的中点,O为AC中点,连接B1O交EF于O1,
(1)求证:D1O1⊥B1O
(2)求二面角D1-AC-B1的正切值。
18.(13分)
已知数列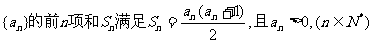
(1)求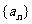 的通项公式;
的通项公式;
(2)若对任意的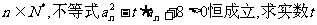 的取值范围。
的取值范围。
17.(13分)
大学毕业的小张到甲、乙、丙三个不同的单位应聘,各单位是否录用他相互独立,其被录用的概率分别为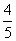 、
、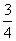 、
、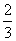 (允许小张被多个单位同时录用)
(允许小张被多个单位同时录用)
(1)小张没有被录用的概率;
(2)设录用小张的单位个数为ξ,求ξ的分布列和它的数学期望。
16.(13分)
已知A、B、C为△ABC的三内角,且其对边分别为a、b、c,若
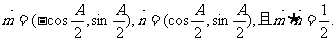
(1)求角A;
|
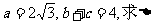 ABC的面积。
ABC的面积。湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com