
22.已知函数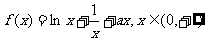 (
(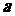 为实常数)
为实常数)
(1)当 时,求
时,求 最小值;
最小值;
(2)若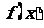 在
在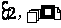 是单调函数,求
是单调函数,求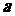 的取值范围;
的取值范围;
(3)设各项为正的无穷数列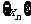 满足
满足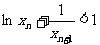 ,证明:
,证明: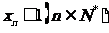 .
.
21.设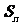 是正项数列
是正项数列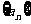 的前
的前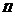 项和,且
项和,且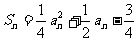 .
.
(1)求数列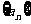 的通项公式;
的通项公式;
(2)是否存在等比数列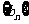 ,使
,使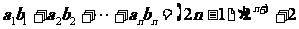 对一切正整数都成立?并证明你的结论.
对一切正整数都成立?并证明你的结论.
(3)设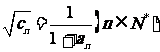 ,且数列
,且数列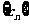 的前
的前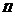 项和为
项和为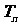 ,试比较
,试比较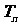 与
与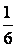 的大小.
的大小.
20.椭圆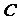 的中心在原点
的中心在原点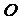 ,它的短轴长为
,它的短轴长为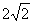 ,相应的焦点
,相应的焦点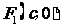 (
(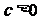 )的准线
)的准线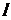 与
与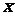 轴相交于
轴相交于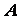 ,
,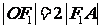 .
.
(1)求椭圆的方程;
(2)过椭圆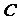 的左焦点作一条与两坐标轴都不垂直的直线
的左焦点作一条与两坐标轴都不垂直的直线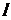 ,交椭圆于
,交椭圆于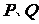 两点,若点
两点,若点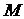 在
在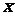 轴上,且使
轴上,且使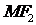 为
为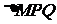 的一条角平分线,则称点
的一条角平分线,则称点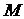 为椭圆的“左特征点”,求椭圆
为椭圆的“左特征点”,求椭圆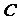 的左特征点;
的左特征点;
(3)根据(2)中结论,猜测椭圆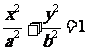 左特征点位置.
左特征点位置.
19.(本小题满分12分)四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E点满足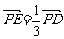 .
.
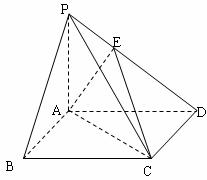
(I)求证:PA⊥平面ABCD; (II)求二面角E-AC-D的大小;
(III)在线段BC上是否存在点F使得PF∥面EAC?若存在,确定F的位置;若不存在,请说明理由。
18.(本小题满分12分)
某高校自愿献血的50位学生的血型分布的情况如下表:
|
血型 |
A |
B |
AB |
O |
|
人数 |
20 |
10 |
5 |
15 |
(Ⅰ)从这50位学生中随机选出2人,求这2人血型都为A型的概率;
(Ⅱ)从这50位学生中随机选出2人,求这2人血型相同的概率;
(Ⅲ)现有一位血型为A型的病人需要输血,要从血型为A,O的学生中随机选出2人准备献血,记选出A型血的人数为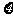 ,求随机变量的分布列及数学期望.
,求随机变量的分布列及数学期望.
17.(12分)已知△ABC的面积S满足3≤S≤3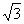 且
且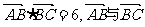 的夹角为
的夹角为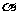 ,
,
(Ⅰ)求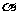 的取值范围;
的取值范围;
(Ⅱ)求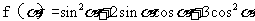 的最小值。
的最小值。
16.下面有五个命题:
①函数y=sin4x-cos4x的最小正周期是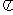 .②终边在y轴上的角的集合是{a|a=
.②终边在y轴上的角的集合是{a|a=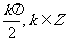 }.
}.
③在同一坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点.
④把函数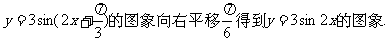
⑤函数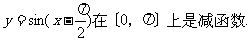
所有正确命题的序号是 .(把你认为正确命题的序号都填上)
15.已知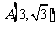 ,
,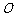 为原点,点
为原点,点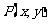 的坐标满足
的坐标满足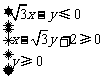 ,则
,则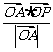 的最大值是 ___,此时点
的最大值是 ___,此时点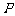 的坐标是 _____.
的坐标是 _____.
14.已知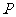 是直线
是直线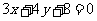 上的动点
上的动点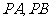 是圆
是圆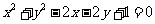 的两条切线,
的两条切线,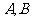 是切点,
是切点,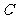 是圆心,那么四边形
是圆心,那么四边形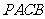 面积的最小值时,弦
面积的最小值时,弦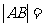 ;
;
13.在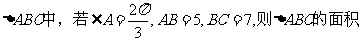 = ;
= ;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com