21．(本小题满分14分)

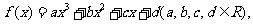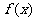　　　 已知函数且函数的图象关于原点对称，其图象在x=3处的切线方程为。

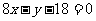　 (1)求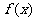的解析式；

　 　(2)是否存在区间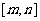，使得函数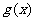的定义域和值域均为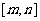，且其解析式为　　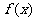　　 的解析式？若存在，求出这样的一个区间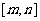；若不存在，则说明理由。

20．(本小题满分12分)

　　　 已知斜三棱柱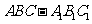，∠BCA=90°，AC=BC=2，A₁在底面ABC上的射影恰为AC的中点D，又知BA₁⊥AC₁。

　 (Ⅰ)求证AC₁⊥A₁BC；

　 (Ⅱ)求CC₁到平面A₁AB的距离；

　 (Ⅲ)求二面角A-A₁B-C的大小。

19．(本小题满分12分)

一个正四面体的四个面上分别涂有1，2，3，4四个数字，现随机投掷两次，正四面体面朝下的数字分别为x₁、x₂，记=(x₁-3)²+(x₂-3)²。

　 (1)分别求出取得最大值和最小值时的概率；

　 (2)求的分布列及数学期望。

18．(本小题满分12分)

　　　 已知数列{a_n}，其前n项和S_n满足S_n+1=2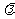S_n+1(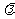是大于0的常数)，且a₁=1，a₃=4.

　 (Ⅰ)求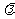的值；

　 (Ⅱ)求数列{a_n}的通项公式a_n；

　 (Ⅲ)设数列{na_n}的前n项和为T_n，试比较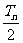与S_n的大小。

17．在锐角△ABC中，已知内角A、B、C所对的边分别为a、b、c，向量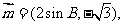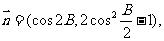且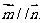

　 (Ⅰ)求角B的大小；

　 (Ⅱ)如果b=2，△ABC的面积S_△ABC的最大值。

16．不等式组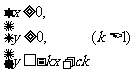所表示的平面区域为D，若D的面积为S，则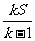的最小值为__________。

15．设直线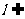平面a，过平面a外一点A作直线，与l, a都成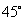角的直线有________条。

14．一对酷爱运动的年轻夫妇，让刚满十个月大的婴儿把“0，0，2，8，北，京”六张卡片排成一排，若婴儿能使得排成的顺序为“2008北京”或“北京2008”，则受到父母的夸奖，那么婴儿受到夸奖的概率为　　　　　 。

13．若抛物线y²=2px的焦点与椭圆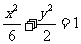的右焦点重合，则p的值为　　　 。

12．若f(x+y)=f(x)f(y)+ f(x)+ f(y)，且f(1)=1则f(1)+ f(2)+…+ f(2009)等于 (　　 )

　　　 A．2²⁰⁰⁹-1　　　　　　　　 B．2²⁰¹⁰-1　　　　　　　　 C．2²⁰⁰⁹-2010　　　　　 D．2²⁰¹⁰-2011