
5.若直线 有两个公共点,则k的取值范围是( )
有两个公共点,则k的取值范围是( )
A.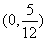 B.
B.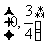 C.
C. D.
D.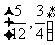
4.已知-9,m,n,-1四个实数成等差数列,-9,a,b,c,-1五个实数成等比数列,则 ( )
( )
A.8 B.-8 C.±8 D.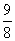
3.在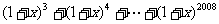 的展开式中,
的展开式中, 的系数是 ( )
的系数是 ( )
A.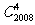 B.
B.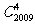 C.
C.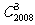 D.
D.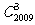
2.已知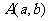 是直线
是直线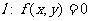 上的一点,
上的一点,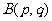 是直线l外一点,由方程
是直线l外一点,由方程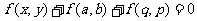 表示的直线与直线l的位置关系是 ( )
表示的直线与直线l的位置关系是 ( )
A.斜交 B.垂直 C.平行 D.重合
1.已知集合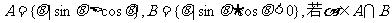 ,则
,则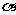 所在的象限是 ( )
所在的象限是 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
22.(本小题满分12分)
(理科做)已知函数 f(x)=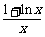 (x≥1).
(x≥1).
(Ⅰ)试判断f(x)的单调性,并说明理由;
|
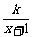 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;
(Ⅲ)求证: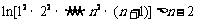 .
.
(文科做)已知函数f(x)=x3+ax2+bx+c,过曲线y=f(x)上的点P(1,f(1))的切线方程为y=3x+1.
(Ⅰ)若函数f(x)在x=-2处有极值,求f(x)的表达式;
(Ⅱ)若函数y=f(x)在区间[-2,1]上单调递增,求实数b的取值范围.
21.(本小题满分12分)
已知直线y=-x+1与椭圆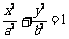 (a>b>0)相交于A、B两点,且线段AB的中点在直线l:x-2y=0上.
(a>b>0)相交于A、B两点,且线段AB的中点在直线l:x-2y=0上.
(Ⅰ)求此椭圆的离心率;
(Ⅱ)若椭圆的右焦点关于直线l的对称点在圆x2+y2=4上,求此椭圆的方程.
20.(本小题满分12分)
已知函数f(x)=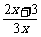 ,数列{An}满足a1=1,an+1= f(
,数列{An}满足a1=1,an+1= f(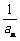 ),nÎN*.
),nÎN*.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)(理科做)令bn= (n≥2),b1=
(n≥2),b1=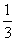 ,Sn=b1+b2+···+ bn,若Sn<
,Sn=b1+b2+···+ bn,若Sn<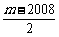 对一切nÎN*成立,求最小正整数m.
对一切nÎN*成立,求最小正整数m.
(文科做)令bn=(a2n-1-a2n+1)a2n,求数列{bn}的前n项和Tn.
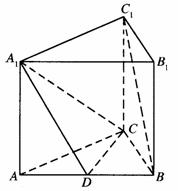
19.(本小题满分12分)
如图,在直三棱柱A1B1C1-ABC中,AC⊥CB,D为AB中点,CB=1,AC=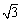 ,A1A=
,A1A=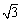 .
.
(Ⅰ)求证:BC1∥平面A1CD;
(Ⅱ)求二面角A-A1C-D的大小.
18.(本小题满分12分)
某射击比赛规则是:开始时在距离目标100米处射击,如果命中记3分,同时停止射击;若第一次射击未命中目标,则可以进行第二次射击,但目标已在150米处,这时命中记2分,同时停止射击;若第二次射击仍未命中目标,还可以进行第三次射击,此时目标已在200米远处,这时命中记1分,同时停止射击;若三次射击都未命中目标,则记0分.已知甲射手在100米处击中目标的概率是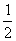 ,他命中目标的概率与距离的平方成反比,且各次射击是相互独立的.
,他命中目标的概率与距离的平方成反比,且各次射击是相互独立的.
(1)求射手甲分别在150米和200米处命中目标的概率;
(2)(理科做)设x为射手甲在该射击比赛中的得分,求Ex.
(文科做)求射手甲在该射击比赛中能得分的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com