
2.抛物线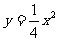 的焦点坐标是 ( )
的焦点坐标是 ( )
A.(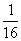 ,0) B.(0,
,0) B.(0,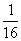 ) C.(0,1) D.(1,0)
) C.(0,1) D.(1,0)
1.设集合A={-1,0,1,2},B=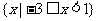 ,则A∩B ( )
,则A∩B ( )
A.{-1,0} B.{-1,0,1} C.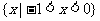 D.
D.
22.(本小题满分14分)
已知斜率为-1的直线l与椭圆C:4x2+5y2=20的交点在y轴右侧。
(1)求l直线的y截距的取值范围;
(2)设AB是过椭圆C中心的任意弦,l′是线段AB的垂直平分线.M是l′上异于椭圆中心的点.
①若|MO|=λ|OA|(O为坐标原点),当点A在椭圆C上运动时,求点M的轨迹方程;
②若M是l′与椭圆C的交点,求△AMB的面积的最小值。
21.(本小题满分12分)在函数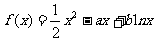 图像上,横坐标为2的点处的切线方程为
图像上,横坐标为2的点处的切线方程为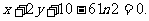
(1)求a、b的值;
(2)讨论方程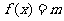 解的情况(相同根算一根)。
解的情况(相同根算一根)。
20.(本小题满分12分)
已知数列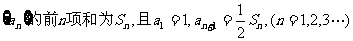 。
。
(1)求数列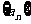 的通项公式;
的通项公式;
(2)当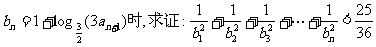 。
。
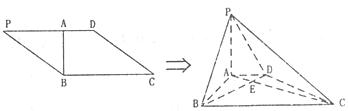
19.(本小题满分12分)如图,在□PBCD中 ,AB⊥PD于A,PA=4,AB=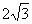 ,BC=6,将△PAB沿AB折起,使PA⊥BC。
,BC=6,将△PAB沿AB折起,使PA⊥BC。
(1)求证:BD⊥平面PAC;
(2)求二面角A-PC-D的大小。
17.(本小题满分12分)已知向量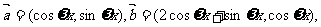 其中
其中 
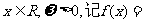
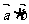 ,且该函数的最小正周期是
,且该函数的最小正周期是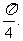
(1)求ω的值;
(2)求函数f(x)的最大值,并且求使f(x)取得最大的值的x的集合。
|
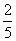 ,第二关通过的概率为
,第二关通过的概率为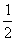 。
。
(1)求他不需要补过就可以获得奖品的概率;
(2)在参加这项活动过程中,假设他不放弃所有的过关机会,记他参加冲关的次数为ξ,求ξ的数学期望Eξ。
16.班主任准备从班上10名男团员,6名女团员中选3人组成一个主委组,则选到的3名同学中既有男团员又有女团员的不同选法共有 种(用数字作答)
15.设函数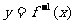 的反函数为
的反函数为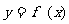 ,且函数
,且函数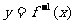 -x的图象过点(-1,2),则函数
-x的图象过点(-1,2),则函数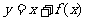 的图象一定过点
。
的图象一定过点
。
14.点P(x,y)满足 则点P到坐标原点距离r的取值范围是
。
则点P到坐标原点距离r的取值范围是
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com